碎石集料变形机理的块体元数值试验分析
马正涛 , 1 , 2 , 3 , 李双洋 , 2 , 赵永春 2 , 李根 2
1.甘肃省公路局, 甘肃 兰州 730000
2.中国科学院 西北生态环境资源研究院 冻土工程国家重点实验室, 甘肃 兰州 730000
3.兰州大学 土木工程与力学学院 西部灾害与环境力学教育部重点实验室, 甘肃 兰州 730000
Deformation process and mechanisms of crushed rock aggregate analyzed by numerical experiment of discrete element method
MA Zhengtao , 1 , 2 , 3 , LI Shuangyang , 2 , ZHAO Yongchun 2 , LI Gen 2
1.Highway Bureau of Gansu Province,Lanzhou 730000,China
2.State Key Laboratory of Frozen Soil Engineering,Northwest Institute of Eco-Environment and Resources,Chinese Academy of Sciences,Lanzhou 730000,China
3.Key Laboratory of Mechanics on Disaster and Environment in Western China,Ministry of Education,College of Civil Engineering and Mechanics,Lanzhou University,Lanzhou 730000,China
通讯作者: 李双洋, 研究员, 从事寒区岩土工程、 防灾减灾工程研究. E-mail: lisy@lzb.ac.cn .
编委: 周成林
收稿日期: 2017-12-19
修回日期: 2018-03-24
基金资助:
国家重点研发计划项目 . 2018YFC0808401 国家自然科学基金项目 . 41672315 中国科学院青年创新促进会优秀会员项目 . Y201975
Received: 2017-12-19
Revised: 2018-03-24
作者简介 About authors
马正涛(1994-),男,甘肃临夏人,助理工程师,2019年在兰州大学获硕士学位,从事路基数值模拟研究.E-mail:m18394818398@163.com
, E-mail:m18394818398@163.com
摘要
块碎石作为道砟材料能够分散列车动荷载, 加之其内部含有大量空隙, 具有良好的对流换热特性, 作为冷却冻土路基的材料在青藏铁路建设中被广泛使用。但在列车荷载的作用下, 碎石集料会发生压密、 变形乃至破碎从而影响冷却效果。因此, 研究碎石层的变形过程及机理具有十分重要的现实意义。基于块体离散元法, 对块碎石集料的三轴剪切试验进行了数值分析, 将所得应力-应变曲线与室内试验结果进行了对比, 发现两者能较好地吻合, 说明块体离散元法能够较好地模拟块碎石集料的受力变形过程。结果表明: 增大围压或块体粒径, 块体单元受到的作用力加强, 集料的偏应力强度和抗剪强度值也随之增大。碎石块体在剪切作用下沿其接触面滑动分离, 形成X形剪切带是集料变形的主要形式, 此外在径向方向出现不同程度的扩张。基于试验和块体元研究路基碎石层的思路和方法可为今后评估青藏铁路碎石路基的热力稳定性提供理论依据和参数储备。
关键词:
块体离散元 碎石集料 冻土路基 应力-应变 X形剪切带
Abstract
As a ballast material, the crushed rock is able to disperse train dynamic load, and it has a distinct characteristic of good convective heat transfer characteristics. Therefore, it was extensively used to cool the permafrost embankment in Qinghai-Tibet Railway. However, the crushed rock layer is compacted and even crushed under train load, so the cooling effect of the crushed rock layer decreases. For this reason, it is very important to study deformation process and mechanisms of the crushed rock layer. In this study, numerical simulations on triaxial tests of the crushed rock were carried out by the discrete element method (DEM). A comparison between experimental and numerical results show they well agree with each other, which implies the DEM can simulate the deformation process of the crushed rock. Moreover, the numerical result indicates that the deviatoric stresses and shear strength values increase with confining pressure and block size. The mainly deformation of the crushed rocks is an X shear band formed by sliding and separating along the contact surface under the shear action. In addition, there are different degrees of expansion in the radial direction. The research idea and method of the crushed rock layer in this study will be useful for evaluating thermodynamic stability of the crushed rock embankment of the Qinghai-Tibet Railway.
Keywords:
discrete element method (DEM) crushed rock aggregate permafrost embankment stress-strain X shear band
本文引用格式
马正涛, 李双洋, 赵永春, 李根. 碎石集料变形机理的块体元数值试验分析 [J]. 冰川冻土 , 2020, 42(4): 1267-1274 doi:10.7522/j.issn.1000-0240.2020.0103
MA Zhengtao, LI Shuangyang, ZHAO Yongchun, LI Gen. Deformation process and mechanisms of crushed rock aggregate analyzed by numerical experiment of discrete element method [J]. Journal of Glaciology and Geocryology
0 引言
碎石材料因取材途径广泛、 使用成本低廉、 以及较高的强度等级常在铁路工程中作为道砟集料, 因其能有效分散列车行驶过程中产生的动力荷载, 所以能有助于降低减弱列车行驶过程中产生的噪音。此外, 碎石集料中含有大量的空隙, 有着较好的对流换热特性, 在青藏铁路的建设过程中作为冷却冻土路基的材料而被广泛使用, 有效地降低了土体温度, 防止路基下的多年冻土发生退化。但块碎石材料的形状不规则及多棱角特性, 加之列车荷载的长期反复挤压作用, 易出现压密破碎情况, 由此将造成碎石材料承载强度下降与降温能力的减弱, 长此以往将直接影响到寒区青藏铁路安全运营。因此, 对碎石集料在荷载作用条件下的变形机理与力学表现展开进一步研究讨论是十分有必要的。
对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论。但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论。针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究。其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响。实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论。在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用。但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状。因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷。
为了真实再现块碎石间的随机接触状态, 揭示块碎石材料中的块体几何尺寸和块体间的相互作用与块碎石集料的变形及力学响应间的联系, 本文依托块体离散元法对块碎石集料的三轴试验展开仿真分析, 用定义的多面体单元和多样的块体间接触模型再现碎石及碎石块体间的相互接触作用, 并对单元与接触作用选取合理的变形模式及破坏准则, 以此来探究块碎石材料在外力作用下, 其承载力强度和位移变形特性与块碎石尺寸大小、 单元间相互作用间的关系。期望本文的研究内容在拓宽碎石集料的细观变形和力学响应分析方法的同时, 就现实工程问题中涉及到的块碎石材料的关键物理力学参数给出参考取值, 为后续用块体元分析方法研究寒区块碎石路基的热-力稳定性提供相关的理论依据和参数参考。
1 块体元分析原理
本文采用块体单元模型实现对碎石集料中的块碎石单元的模拟。块体单元模型由块体单元和节理单元两部分构成, 岩石块体默认是弹性体, 其内部各点的位移可以由力边界条件进行求解, 破坏之前将岩体看成是连续介质, 多数的滑移和破坏都发生在节理上, 其破坏满足摩尔库仑强度准则和抗张拉破坏条件。块体单元之间的接触关系在受力过程中都保持不变, 并且可以通过阻尼参数来描述岩体的阻尼特性[9 ] 。对相互接触的块体, 可以求得在∆ u
∆ F n = k n ∆ u n (1)
∆ F s = k s ∆ u s (2)
式中: k n 、 k s ∆ u n 、 ∆ u s F i M i u ¨ i θ ¨ i
F i = ∑ F i (3)
M i = ∑ e i j x j F j (4)
u ¨ i = F i m (5)
θ ¨ i = M i I (6)
式中: i , j = x , y , z ; e i j x j m 和I 分别代表块体的质量和转动惯量。
块体离散元计算采用动态松弛离散元法, 其基本方程为[10 ] :
m u ¨ t + c u ˙ t + k u ˙ t = f ( t ) (7)
式中: m u t c k f ( t ) t 为时间。一般任意块体的运动方程可表示为:
u ¨ i + c u ˙ i = F i m (8)
θ ¨ i + c θ ˙ i = M i I (9)
对上式进行一阶中心差分可求得t + ∆ t / 2 u ˙ i ( t + ∆ t / 2 ) θ ˙ i ( t + ∆ t / 2 ) t + ∆ t
∆ u i = u ˙ i ( t + ∆ t / 2 ) ∆ t (10)
∆ θ i = θ ˙ i ( t + ∆ t / 2 ) ∆ t (11)
u i t + ∆ t = u i t + ∆ u i (12)
θ i t + ∆ t = θ i t + ∆ θ i (13)
对于可变形的块体单元, 为了研究块体的变形, 对其进行随机地四面体单元划分, 在单元的顶点上建立运动方程[11 ] :
u ¨ i = ∫ S σ i j n j d s + F i m + g i (14)
式中: S 是质量点的外表面; σ i j n j S 的单位法向量; F i ∑ F i ∑ F i
u ˙ i t + ∆ t / 2 = u ˙ i t - ∆ t / 2 + ∑ F i ( t ) ∆ t m (15)
上述整个求解过程基于动态显示差分方法, 在每时步初始时刻, 依据(8)、 (9)运动方程公式, 更新块体的运动状态, 再用中心差分的方法得到位移增量, 以此可更新下一时步的位置。通过位移增量可求得接触力增量, 进一步对块体受力状态完成更新, 结合运动方程再进行下一时步的计算。
2 碎石三轴试验数值模型
2.1 模型建立
为使数值仿真效果能接近室内试验, 依据王鹏程等[12 ] 的试验数据, 建立高为30.5 cm, 外接圆直径为15.25 cm的正三十面棱柱体来模拟三轴试样, 依据室内试验中的两个级配试样(1.27~2.54 cm和2.54~3.81 cm), 通过随机划分生成四面体单元来模拟试验中的碎石块体, 在三轴试样的轴向两端设置相当规格尺寸的加载装置用以施加轴向作用力, 最终建成的三轴试样的模型见图1 。
图1
图1
块体元数值试验模型
Fig.1
Numerical experiment model of discrete element method (DEM), for grading range 1.27~2.54 cm (a) and 2.54~3.81 cm (b)
2.2 块体相关参数
块碎石材料的密度以试验数据(2 650 kg·m-3 )为准。块体的强度参数和块体间的接触参数反复试算, 最终选用的参数值如表1 、 表2 所示。
3 块体离散元数值分析
3.1 应力强度对比分析
图2 、 图3 为1.27~2.54 cm、 2.54~3.81 cm两种级配碎石集料在三种不同围压环境下块体元三轴试验所得到的应力-应变曲线与室内试验结果的比较。结合两种情况对比, 可以发现块体元分析方法得到结果与试验测得的结果吻合较好, 初步表明块体元法用于研究块碎石材料相关力学问题的设想是可行的。
图2
图2
1.27~2.54 cm级配各围压下应力-应变曲线
Fig.2
Deviatoric stress-axial strain curves under confining pressure of 55.1 kPa (a), 103.4 kPa (b), 206.8 kPa (c), experimental and simulated, for grading range 1.27~2.54 cm; together with the three comparison together (d)
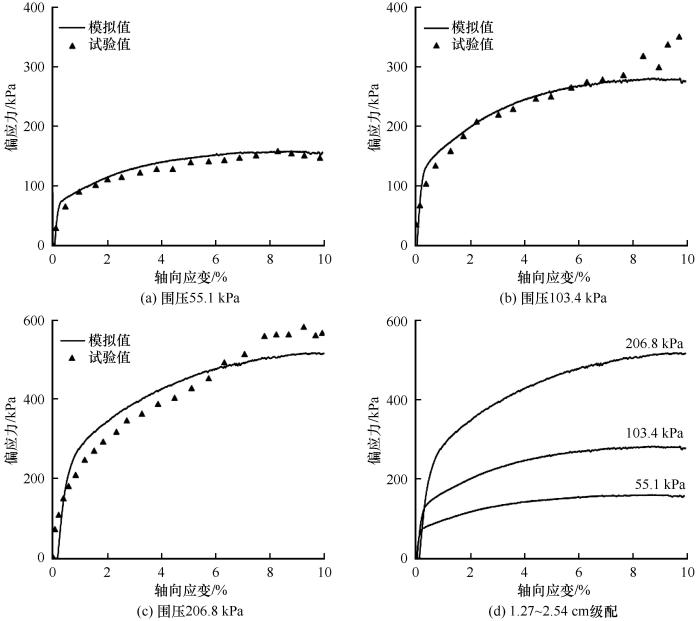
图3
图3
2.54~3.81 cm级配各围压下应力-应变曲线
Fig.3
Deviatoric stress-axial strain curves under confining pressure of 55.1 kPa (a), 103.4 kPa (b), 206.8 kPa (c), experimental and simulated, for grading range 2.54~3.81 cm; together with the three comparison together (d)
观察图2 (d)、 图3 (d), 看出相同的轴向应变条件下, 试样侧向围压从55.1 kPa增大到206.8 kPa, 使块体间的相互作用增强, 集料偏应力强度增大。从图2 (d)中不同围压条件下的应力-应变曲线可以得出, 当侧向应力为55.1 kPa时, 轴向应变超过4%, 集料的偏应力强度值趋近于150 kPa; 当侧向应力增加至103.4 kPa, 应变超过6%, 偏应力强度达到250 kPa; 侧向围压提升至206.8 kPa, 且轴向应变达到10%后, 轴向应变继续增加, 偏应力强度也继续增大, 未出现较明显的极值。该情况表明偏应力强度最大值随着侧向应力的增大出现延迟现象, 图3 (d)中也有相类似的情况, 这是因为碎石块体在受到侧向围压的作用后, 其在径向方向自由运动受到限制, 这种限制作用在随侧向围压增大而加强, 一定程度上降低减小块体间因挤压作用而滑动、 分离的运动趋势。但这种相互挤压作用随轴向应变的增加而加强, 试样中的部分块体相对静止状态最终达到临界条件, 在块体间的接触面上, 发生滑移以及错动, 以至于相互分离, 这就使得相邻块体的相互作用消失, 碎石试样的偏应力强度值不再增长, 并趋于稳定。
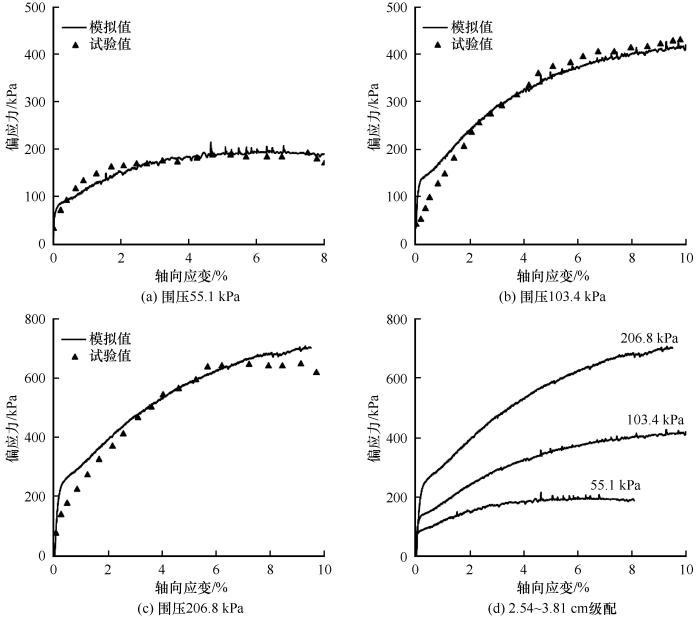
图4 记录的是块体三轴试样在试验结束后不同侧向围压下的偏应力强度值的对比, 从图中数据可以得出随试样侧向应力的增加, 不同级配的集料的偏应力强度值从150 kPa、 200 kPa, 增加到500 kPa、 700 kPa, 表明集料的承载力强度随围压的增长而提高。因侧向应力的增加致使块体间的作用力增大, 碎石单元的应力强度增长, 碎石试样的偏应力强度值增大。相同围压下碎石试样, 粒径尺寸越大, 加载结束后得到的偏应力强度就越大, 其原因是块体尺寸越大单元间接触面积越大, 接触力越大, 单元的主应力值就更大, 块碎石试样的偏应力强度值就更高。
图4
图4
不同围压下的最大偏应力强度
Fig.4
Deviatoric stress changing with confining pressures for grading range 1.27~2.54 cm and 2.54~381 cm
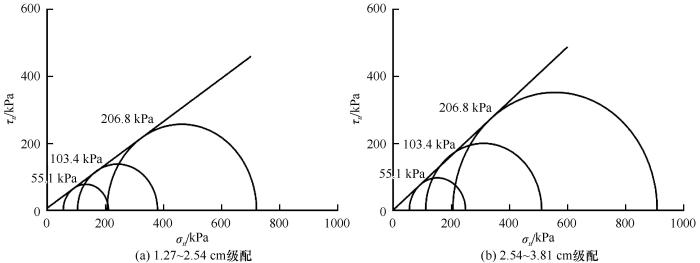
如图5 所示, 根据数值分析得到的应力强度值, 分别做出两种级配的集料在不同围压强度下的莫尔应力圆, 并在此基础上做出莫尔强度包络线。从图中包络线可以得到块碎石集料的内聚力接近为零, 这与块体间只存在相互接触作用, 块体之间实际相分离, 接触面上不存在黏聚力这一实际情况相符合。由图可以得到块碎石集料抗剪强度的最大值随着围压的增加而增长, 这与侧向应力的增大从而限制和减少块碎石在剪切作用下出现分离错动的运动趋势, 块体接触面能承受更强的剪切作用密切相关。对比图5(a) 、 5(b) 中的强度包络线, 在相同σ n
图5
图5
各围压下的莫尔强度包络线
Fig.5
Mohr strength envelopes of various confining pressures for grading range 1.27~2.54 cm (a) and 2.54~3.81 cm (b)
3.2 位移变形分析
图6 为1.27~2.54 cm级配的碎石集料在55.1 kPa围压应力条件下得到的位移矢量图。如图6(a) 、 6(b) 所示, 从开始加载到轴向应变为3%, 试样在轴向方向开始出现变形, 径向方向有轻微的膨胀, 试样中的部分单元仅有很小的转动与滑动。当轴向应变增长到7%, 如图6 (c)所示, 因块体试样轴向应变进一步增大, 试样的变形进一步加剧, 整个三轴模型在径向的位移更加突出, 越来越多的块体与相邻块体间的相互作用减弱。结合图6 (d), 当轴向应变达到10%时, 块碎石集料模型中间的部分块体因挤压作用在径向方向的运动趋势更加明显, 这些块体单元上的作用力不再增加, 集料的偏应力强度值增长趋势减缓。
图6
图6
1.27~2.54 cm级配55.1 kPa位移矢量图
Fig.6
Displacement vector graphs at confining pressure of 55.1 kPa for grading range 1.27~2.54 cm as axial strain of 0% (a), 3% (b), 7% (c) and 10% (d)
碎石试样中的部分块体因剪切作用在块体间的接触面上形成形状为X形的剪切破坏带, 随轴向位移的增加这种变形破坏形式更加明显。因块体间的接触作用力随轴向位移增加而增大, 导致块体单元的运动状态发生改变, 单元沿块体间接触面错动和分离, 运动的块体对相邻块体产生挤压作用, 相邻块体因此作用沿剪切面方向发生滑移和分离, 形成剪切破坏带。随着轴向应变的进一步增长, 这种滑移和分离的变形趋势更加明显, 集料中出现的剪切破坏带随轴向位移的增加而向试样两端及四周延伸趋势更加显著。
4 结论
本文利用块体离散元的数值分析方法, 对块碎石集料的三轴剪切试验进行了数值模拟, 结合室内试验所获得的数据。得到如下结论:
(1) 借助块体离散元的数值分析方法研究了碎石集料三轴剪切试验, 用随机生成的多面体块体单元和块体间任意平面状非规则接触, 实现对块碎石集料和块碎石间接触作用的模拟。对于不同粒径范围的碎石集料, 在三种侧向围压条件下, 块体元法分析获得的结果与试验结果吻合程度较高, 表明用块体元数值方法研究碎石材料力学及变形行为是可行的。
(2) 块碎石试样间的挤压作用因试样所受侧向应力的增加而加强, 这就使碎石试样的偏应力强度值随围压提高而增大; 在围压一致条件下, 块体间的接触面积随粒径尺寸增加而增大, 其结果是块体单元所受外力作用增强, 集料偏应力强度值变大。
(3) 由数值试验数据做出的莫尔强度包络线得到块碎石集料的内聚力接近为零, 这与块体间接触面上无黏聚力相符合。块碎石因围压增长而发生分离错动的趋势减弱, 试样抗剪切能力提高; 块碎石单元尺寸增大, 接触面积增大, 承受的切向力作用更大, 集料的抗剪强度提高。
(4) 在整个试验过程中, 碎石试样模型的主要变形是因部分块体滑动、 错动而形成X形剪切带。随着轴向应变的不断增加, 剪切破坏带不断向两端延伸。试样中的大多数块体因挤压在径向都有不同程度的位移变形, 位于试样中间的块体这种运动趋势越发显著。此外, 碎石试样的应力强度也因块体间接触力不再增长而达到极值。
上述结论包含了两种级配的碎石集料在不同的围压条件下, 其应力强度与变形破坏方面的相关规律, 并从微观角度解释了块体尺寸和侧向应力的变化与试样应力强度、 位移变形间的联系, 一定程度上反映出块体元分析方法研究碎石集料力学行为和变形的可行性。然而, 真实的块体形状往往具有多样性与复杂性, 本文采用单一的接触滑移准则, 没有考虑到接触面的粗糙度以及不平整性对碎石集料的强度和变形所产生的影响。因此需要在下一步的工作中不断完善和优化模型, 进一步研究非规则形状碎石块体和复杂的应力作用下块碎石的强度及其变形破坏。为今后利用块体离散元法研究青藏铁路碎石路基的热力稳定性定量评估奠定理论基础。
参考文献
View Option
[1]
Ghanbari A Sadeghpour A H Mohamadzadeh H An experimental study on the behavior of rockfill materials using large scale tests
[J]. Electronic Journal of Geotechnical Engineering , 2008 , 13 (1 ): 1 - 16 .
[本文引用: 1]
[2]
Suiker A S J Selig E T Frenkel R Static and cyclic triaxial testing of ballast and subballsat
[J]. Journal of Geotechnical and Geoenvironmental Engineering , 2005 , 131 (6 ): 771 - 782 .
[本文引用: 1]
[3]
Liu Mengcheng Gao Yufeng Liu Hanlong Study on shear dilatancy behaviors of rockfills in large-scale triaxial tests
[J]. Chinese Journal of Geotechnical Engineering , 2008 , 30 (2 ): 205 - 211 .
[本文引用: 1]
刘萌成 , 高玉峰 , 刘汉龙 堆石料剪胀特性大型三轴试验研究
[J]. 岩土工程学报 , 2008 , 30 (2 ): 205 - 211 .
[本文引用: 1]
[4]
Lim W L Mechanics of railway ballsat behaviour
[D]. Nottingham : University of Nottingham , 2004 .
[本文引用: 1]
[5]
Sun Y Indraratna B Nimbalkar S Three-dimensional characterization of particle size and shape for ballast
[J]. Geotechnique Letters , 2014 , 4 (3 ): 197 - 202 .
[本文引用: 1]
[6]
Indraratna B Ngo N T Rujikiatkamjorn C et al Behavior of fresh and fouled railway ballast subjected to direct shear texting: discrete element simulation
[J]. International Journal of Geomechanics , 2014 , 14 (1 ): 34 - 44 .
[本文引用: 1]
[7]
Lu M McDowell G R The importance of modelling ballast particle shape in the discrete element method
[J]. Granular Matter , 2007 , 9 (12 ): 69 - 80 .
[本文引用: 1]
[8]
Kong Liang Peng Ren Particle flow simulation of influence of particle shape on mechanical properties of quasi-sands
[J]. Chinese Journal of Rock Mechanics and Engineering , 2011 , 30 (10 ): 2112 - 2119 .
[本文引用: 1]
孔亮 , 彭仁 颗粒形状对类砂土力学性质影响的颗粒流模拟
[J]. 岩石力学与工程学报 , 2011 , 30 (10 ): 2112 - 2119 .
[本文引用: 1]
[9]
Tian Zhennong Li Shihai Liu Xiaoyu et al Research on deformable calculation method based on three-dimensional block discrete element
[J]. Chinese Journal of Rock Mechanics and Engineering , 2008 , 27 (): 2832 - 2840 .
[本文引用: 1]
田振农 , 李世海 , 刘晓宇 , 等 三维块体离散元可变形计算方法研究
[J]. 岩石力学与工程学报 , 2008 , 27 (): 2832 - 2840 .
[本文引用: 1]
[10]
Cai Meifeng Rock mechanics and engineering [M]. 2nd ed . Beijing : Science Press , 2002 .
[本文引用: 1]
蔡美峰 岩石力学与工程 [M]. 2版 . 北京 : 科学出版社 , 2002 .
[本文引用: 1]
[11]
Shi Chong Chu Weijiang Zheng Wenshang Simulation technology and engineering application of block discrete element [M]. Beijing : China Architecture & Building Press , 2016 .
[本文引用: 1]
石崇 , 褚卫江 , 郑文棠 块体离散元数值模拟技术及工程应用 [M]. 北京 : 中国建筑工业出版社 , 2016 .
[本文引用: 1]
[12]
Wang Pengcheng Study on the strength and deformation characteristics of crushed rock aggregate
[D]. Beijing : Beijing Jiaotong University , 2016 .
[本文引用: 1]
王鹏程 碎石集料强度与变形特性的研究
[D]. 北京 : 北京交通大学 , 2016 .
[本文引用: 1]
[13]
Zhou Xianqi Xu Weiya Niu Xinqiang et al A review of distinct element method researching progress and application
[J]. Rock and Soil Mechanics , 2007 , 28 (): 408 - 416 .
周先齐 , 徐卫亚 , 钮新强 , 等 离散单元法研究进展及应用综述
[J]. 岩土力学 , 2007 , 28 (): 408 - 416 .
[14]
Li Shihai Wang Yuannian Selection study of computational parameters for DEM in geomechanics
[J]. Chinese Journal of Rock Mechanics and Engineering [J]. Chinese Journal of Rock Mechanics and Engineering, 2004 , 23 (21 ): 3642 - 3651 .
李世海 , 汪远年 三维离散元计算参数选取方法研究
[J]. 岩石力学与工程学报 , 2004 , 23 (21 ): 3642 - 3651 .
[15]
Liu Kaixin Gao Lingtian A review on the discrete element method
[J]. Advances in Mechanics , 2003 , 33 (4 ): 483 - 490 .
刘凯欣 , 高凌天 离散元法研究的评述
[J]. 力学进展 , 2003 , 33 (4 ): 483 - 490 .
[16]
Zhengtao Mang Numerical simulation of thermal-dynamical responses of crushed rock embankment in permafrost regions
[D]. Lanzhou : Lanzhou University , 2019 .
马正涛 多年冻土区块碎石路基热-动力响应数值仿真研究
[D]. 兰州 : 兰州大学 , 2019 .
An experimental study on the behavior of rockfill materials using large scale tests
1
2008
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Static and cyclic triaxial testing of ballast and subballsat
1
2005
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Study on shear dilatancy behaviors of rockfills in large-scale triaxial tests
1
2008
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
堆石料剪胀特性大型三轴试验研究
1
2008
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Mechanics of railway ballsat behaviour
1
2004
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Three-dimensional characterization of particle size and shape for ballast
1
2014
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Behavior of fresh and fouled railway ballast subjected to direct shear texting: discrete element simulation
1
2014
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
The importance of modelling ballast particle shape in the discrete element method
1
2007
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Particle flow simulation of influence of particle shape on mechanical properties of quasi-sands
1
2011
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
颗粒形状对类砂土力学性质影响的颗粒流模拟
1
2011
... 对块碎石集料宏观承载强度特性及破坏模式研究通常是以岩石力学室内试验方法为主, Ghanbari等[1 ] 利用大型三轴试验和直剪试验对碎石集料的力学性能展开研究, 得到级配良好的碎石集料的摩擦角与承载力更大, Suiker[2 ] 依托动、 静三轴剪切实验, 发现循环荷载作用条件下, 散体道砟材料的强度和刚度得到改善; 刘萌成等[3 ] 、 Lim[4 ] 、 Sun等[5 ] 利用相关试验设备与传统力学试验研究了碎石材料的力学性质, 得到了不少有关碎石集料变形破坏与力学表现方面的结论.但室内试验的研究内容主要以碎石材料承载强度及变形破坏为主, 对受力变形过程中碎石材料的细观力学响应及变形未展开研究讨论.针对这方面问题, 有研究人员基于以离散元方法开发、 用于模拟研究颗粒介质相互作用和运动的软件PFC, 对碎石材料的力学特性及变形机理开展了不少针对性研究.其中, Indraratna等[6 ] 、 Lu等[7 ] 借助PFC中的clump算法, 开发出可生成不规则形状地多面体颗粒流分析程序, 并以此分析程序研究了块碎石集料的力学响应, 通过与室内试验结果进行对比, 表明PFC分析程序对碎石材料力学行为的模拟仿真效果较为可靠; 孔亮等[8 ] 基于PFC2D, 以4种形状不同的颗粒组为研究对象, 分析了颗粒形状对类沙土材料力学性能的影响.实际上, 颗粒流分析方法作为离散元分析方法的一种, 通过生成不同数量的颗粒单元, 并以单元的运动、 单元与其它单元间的接触挤压, 实现对研究对象变形破坏特性的讨论.在各类型土体试验、 岩体破裂损伤、 矿山崩塌开采等诸多岩土工程复杂变形及细观力学响应等问题的研究中被广泛使用.但是在颗粒流分析方法中所使用颗粒单元及黏结得到的颗粒模型, 与实际的块碎石材料在形状方面尚有差异, 无法真实反映块体几何形状.因此, 了解掌握碎石集料的应力强度及变形特征与碎石单元形状尺寸、 单元间的细观力学行为之间的关系, 颗粒流的分析方法存在着先天缺陷. ...
Research on deformable calculation method based on three-dimensional block discrete element
1
2008
... 本文采用块体单元模型实现对碎石集料中的块碎石单元的模拟.块体单元模型由块体单元和节理单元两部分构成, 岩石块体默认是弹性体, 其内部各点的位移可以由力边界条件进行求解, 破坏之前将岩体看成是连续介质, 多数的滑移和破坏都发生在节理上, 其破坏满足摩尔库仑强度准则和抗张拉破坏条件.块体单元之间的接触关系在受力过程中都保持不变, 并且可以通过阻尼参数来描述岩体的阻尼特性[9 ] .对相互接触的块体, 可以求得在∆ u
三维块体离散元可变形计算方法研究
1
2008
... 本文采用块体单元模型实现对碎石集料中的块碎石单元的模拟.块体单元模型由块体单元和节理单元两部分构成, 岩石块体默认是弹性体, 其内部各点的位移可以由力边界条件进行求解, 破坏之前将岩体看成是连续介质, 多数的滑移和破坏都发生在节理上, 其破坏满足摩尔库仑强度准则和抗张拉破坏条件.块体单元之间的接触关系在受力过程中都保持不变, 并且可以通过阻尼参数来描述岩体的阻尼特性[9 ] .对相互接触的块体, 可以求得在∆ u
1
2002
... 块体离散元计算采用动态松弛离散元法, 其基本方程为[10 ] : ...
1
2002
... 块体离散元计算采用动态松弛离散元法, 其基本方程为[10 ] : ...
1
2016
... 对于可变形的块体单元, 为了研究块体的变形, 对其进行随机地四面体单元划分, 在单元的顶点上建立运动方程[11 ] : ...
1
2016
... 对于可变形的块体单元, 为了研究块体的变形, 对其进行随机地四面体单元划分, 在单元的顶点上建立运动方程[11 ] : ...
Study on the strength and deformation characteristics of crushed rock aggregate
1
2016
... 为使数值仿真效果能接近室内试验, 依据王鹏程等[12 ] 的试验数据, 建立高为30.5 cm, 外接圆直径为15.25 cm的正三十面棱柱体来模拟三轴试样, 依据室内试验中的两个级配试样(1.27~2.54 cm和2.54~3.81 cm), 通过随机划分生成四面体单元来模拟试验中的碎石块体, 在三轴试样的轴向两端设置相当规格尺寸的加载装置用以施加轴向作用力, 最终建成的三轴试样的模型见图1 . ...
碎石集料强度与变形特性的研究
1
2016
... 为使数值仿真效果能接近室内试验, 依据王鹏程等[12 ] 的试验数据, 建立高为30.5 cm, 外接圆直径为15.25 cm的正三十面棱柱体来模拟三轴试样, 依据室内试验中的两个级配试样(1.27~2.54 cm和2.54~3.81 cm), 通过随机划分生成四面体单元来模拟试验中的碎石块体, 在三轴试样的轴向两端设置相当规格尺寸的加载装置用以施加轴向作用力, 最终建成的三轴试样的模型见图1 . ...
A review of distinct element method researching progress and application
0
2007
Selection study of computational parameters for DEM in geomechanics
0
2004
A review on the discrete element method
0
2003
Numerical simulation of thermal-dynamical responses of crushed rock embankment in permafrost regions
0
2019
多年冻土区块碎石路基热-动力响应数值仿真研究
0
2019


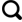





 甘公网安备 62010202000676号
甘公网安备 62010202000676号