0 引言
煤层气是一种非常规天然气, 与煤相伴而生赋存于煤层之中。作为一种新型能源, 煤层气资源具有很大的发展潜力。由于煤层储气层渗透率往往较低, 且煤层具有低孔、 低压的特点, 使得煤层气开采难度增大、 开采效率降低, 必须采取工程措施以提高煤层气的开采量。目前, 最常用的方法是水力压裂技术, 但由于不同地域的煤层具有不同的地质特征, 水力压裂技术不能适用于所有的煤层。如果将人工冻结技术引入煤层改造之中, 通过冰水相变拓展、 贯通裂纹, 形成裂纹网络, 进而可达到增加煤层气产出的效果。
冻结煤岩与冻土有着紧密的联系, 但又存在着明显的差异, 其根本区别在于煤岩体中存在裂隙, 裂隙将整个岩体分割成不连续的块体, 因而不能用连续介质力学方法(如有限元法)来模拟岩体的力学变形行为。同时, 由于裂隙中冰的胶结或润滑作用, 不断地改变了岩体的力学性质及变形特性[6-8], 因此, 冻结煤岩的损伤破坏过程更为复杂。早期的研究大多通过宏观试验来分析岩体的力学变形行为, 如进行岩体的单轴压缩、 单轴拉伸、 常规三轴、 剪切、 劈裂试验等条件力学性质方面的研究[9-12]。此外, 代高飞等[13]利用CT成像技术研究了脆性煤岩单轴压缩破坏全过程的细观损伤规律; 杨永杰等[14]基于MTS试验机和扫描电镜, 从强度和变形特性的角度研究了煤岩的微细观演化过程。这些研究在一定程度上揭示了煤岩在荷载作用下损伤演化特性。
随着计算机技术的发展, 人们更多地依赖计算机模拟手段来分析加卸载条件下裂隙岩体的变形、 强度与破坏特性。唐春安等[15-16]研发了RFPA软件, 将岩体材料性质引入到数值模拟中, 实现了对岩体破坏过程的全程模拟。钟卫平等[17-18]运用ANSYS软件对裂隙岩体在压剪荷载作用下的应力场及位移场进行了数值模拟研究, 并利用断裂力学理论分析了纯剪切应力状态和双向压应力状态作用下岩体的断裂机制。还有一些能量判别准则被提出并引入到数值模拟中, 从而实现了煤岩体损伤及裂纹扩展的模拟[19-21]。以上对裂隙岩体的计算模拟都采用了基于连续介质理论的有限元方法, 对裂隙岩体的损伤破坏过程及力学性质有了一定的认识。但是有限元方法受限于连续介质的假设, 对于裂隙岩体这种非完全连续又非完全散体的结构来说, 存在一定的限制条件。
本文从非连续介质理论角度出发, 采用离散元方法, 对冻结裂隙煤岩在加载条件下的变形、 强度及破坏特性进行数值分析, 并标定煤岩的细观力学参数, 以期通过本文的研究可以从非连续介质理论对冻结裂隙煤岩的力学性质及破坏机理进行分析, 为进一步拓宽离散元的应用领域, 并为今后裂隙煤岩或煤层气开采方面的研究提供参考。
1 离散元数值模拟理论
煤岩是一种介于非连续介质又非完全散体介质之间的特殊材料, 由于其特殊的形成过程及后期的地质运动, 使得煤岩体中包含着大量的裂隙、 节理、 破碎带甚至是断层等不连续的结构, 这使得煤岩既不完全连续, 也不完全散体。若仅用传统的连续介质力学去解释岩体裂隙、 节理、 破碎断裂等非连续力学行为, 则会导致分析结果与实际状态之间存在较大差异。本文使用离散元模拟的方法来描述这种不完全属于连续介质的材料, 把裂隙煤岩看成是由离散的煤块和煤块间的节理面组成的材料, 煤块既能移动、 转动和变形, 节理面也可以被压缩、 分离或滑动, 从而可以较为真实的模拟煤岩中的不连续面。
1.1 受力分析
由于离散单元法将煤岩看成是由单独的煤块通过节理面连接而成的材料, 所以需要描述煤块与煤块间的力学接触行为。在离散元理论中, 相互接触的分散块体间的相对运动会在连接处产生力和力矩, 并作用在相互连接的块体上, 因此, 与该模型相对应的接触力可以分解为在节理面上的法向力Fn 和切向力Fs, 如图1(a)。
图1
图1
离散块体受力分析
Fig.1
Force analysis of discrete blocks: between two blocks (a) and for a single block (b)
在位移ΔU内弹性力增量为:
式中: kn 表示接触处的法向刚度; ks 表示接触处的切向刚度; ΔUn 表示接触处的法向位移; ΔUs 表示接触处的切向位移。
单就一个块体来说, 其受力状况如图1(b), 相应的运动方程如下:
块体上的合力为:
合力矩为:
加速度为:
角加速度:
式中: F表示合力; Fi 表示分力; M表示总力矩; eij 表示基矢量; xj 表示矢径;
1.2 运动方程
离散元的求解方法可分为静态松弛法和动态松弛法。本文采用动态松弛法, 动态松弛法是为解决隐式问题引入的方法, 采用向后时步迭代的计算思想, 把非线性静力学问题转化为动力学问题。该方法实质就是对临界阻尼振动方程进行逐步积分。动态松弛法的基本运动方程如下:
式中: u表示块体形心的位移; μ表示黏性阻尼系数; k表示刚度系数; f表示块体所受的外荷载; t表示时间。
块体离散单元法的求解过程不涉及到大型矩阵运算, 比较简单、 稳定, 因此可以节省计算时间, 同时允许单元发生大位移, 克服了传统有限元方法和边界单元法的小变形假设, 用来求解非线性问题十分方便。
1.3 强度准则
岩体破坏遵循Mohr-Coulomb基本准则, 如图2所示, 图中曲线A到B点的屈服包络线f(σ1,σ3)=0对应的Mohr-Coulomb剪切屈服准则
图2
曲线B点到C点对应的拉破坏准则
式中: φ表示内摩擦角; c表示黏聚力; σt 表示岩体的抗拉强度; 其中
如果岩体的抗拉强度比σ3小, 根据图2中的
由于煤岩属于节理结构的岩体, 因此选用能描述岩体内部节理的节理面接触-库伦滑移理论, 来模拟岩体中的裂隙、 断层及层面。对于完整结构面所受的法向应力满足下式:
式中: Tmax表示破坏面上的拉力; σ表示节理面的抗拉强度; Ac 表示节理面面积。
结构面所受的最大剪力应满足:
式中:
2 煤岩的离散元数值试验
图3
图3
煤柱试验与数值模型
Fig.3
Photos of the MTS testing machine (a), the sample (b) and the damaged sample (c), together with a discrete element model (d)
根据地质勘查报告, 可知岩样的初始物理参数如表1。
表1 岩样的初始物理参数
Table 1
| 天然密度ρ/(kg·m-3) | 天然含水量/% | 饱和密度ρsat/(kg·m-3) | 饱和含水量/% | 干密度ρd/(kg·m-3) | 孔隙度/% |
|---|---|---|---|---|---|
| 1 441.4 | 1.0539 | 1 476.6 | 3.5253 | 1 426.4 | 5.0283 |
2.1 几何数值模型
图4
图4
煤样CT扫描图像
the lower middle section(c)of the coal sample
Fig.4
CT images of the upper middle section (a), the middle section (b) and
2.2 数值模型参数
离散元数值试验是通过模型参数得到的结果来逼近室内试验的结果, 模型细观参数的选取不能直接采用宏观试验参数, 需要反复调试细观参数直至模拟曲线接近试验数据。表2中列出了不同温度下煤岩单轴压缩试验的模拟细观参数, 其中K为体积模量, G为剪切模量。
表2 离散元模型计算参数
Table 2
| 物理量 | K/MPa | G/MPa | c/MPa | φ/(°) | σt /MPa | kn /MPa | ks /MPa | Cres /kPa | φ/(°) |
|---|---|---|---|---|---|---|---|---|---|
| -15 ℃ | 343.5 | 257.6 | 1.29 | 37 | 1.7 | 50.0 | 50.0 | 5.0 | 33 |
| -10 ℃ | 314.8 | 236.1 | 1.26 | 35 | 1.5 | 37.7 | 37.7 | 4.4 | 31 |
| -4 ℃ | 287.7 | 215.8 | 1.22 | 33 | 1.3 | 22.9 | 22.9 | 3.7 | 29 |
| 20 ℃ | 259.5 | 194.6 | 1.20 | 32 | 1.2 | 13.0 | 13.0 | 3.2 | 27 |
3 煤岩离散元分析
3.1 应力-应变关系
在-15
图5
图5
不同温度煤岩单轴应力-应变关系曲线
Fig.5
Stress-strain curves of coal samples at -15 ℃ (a), -10 ℃ (b), -4 ℃ (c) and 20 ℃ (d): experimental and simulated
从图5可以看出, 当煤柱的温度为-15
通过以上的分析发现, 随着煤柱温度的降低, 曲线的峰值应力增大。出现这样的现象是因为冻结煤岩中的未冻水会随着温度的降低而逐渐转变成冰, 而未冻水存在于煤岩的微裂隙中, 未冻水的状态变化使得煤岩的微裂隙得到冰的填充。由于煤岩的破坏主要发生在这些微裂隙、 节理面等上, 冰的黏结作用使得这些薄弱连接面得到了加固, 使其不易发生错动, 从而使得煤岩的强度得到提高。同时, 从四条曲线的走势来看, 煤岩的破坏类型均为脆性破坏, 这说明在此温度范围内, 煤岩的破坏类型与温度无关。但是温度的不同使得发生破坏的应变不同。当温度为-15
3.2 位移变化规律
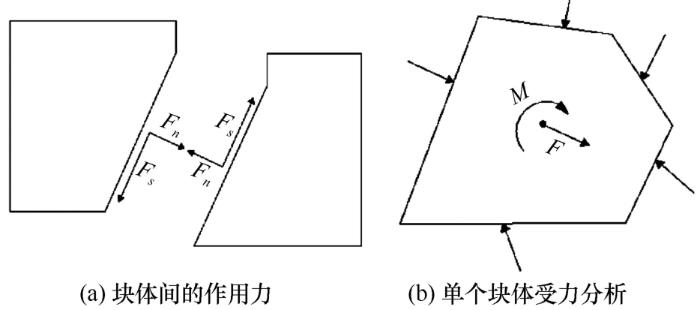
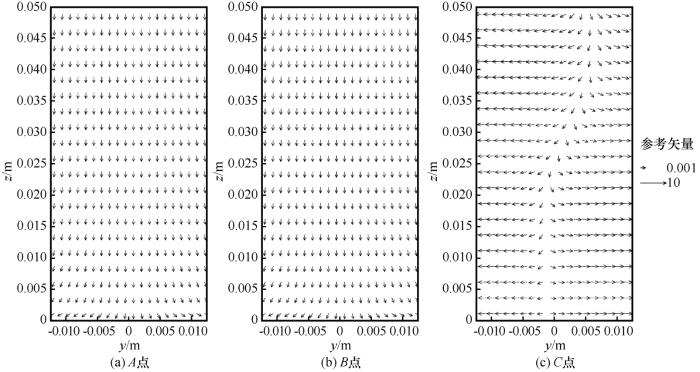
图6给出了温度为-15
图6
图6
-15 ℃煤柱不同变形阶段的变形矢量(mm)
Fig.6
Deformation vector of coal pillar at -15 ℃ at different deformation stages (mm)
图7
图7
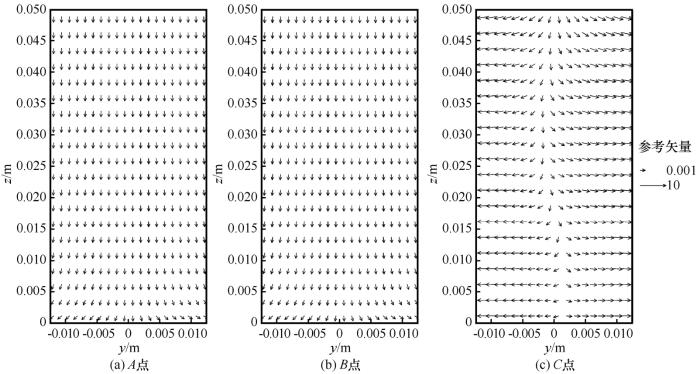
-10 ℃煤柱不同变形阶段的变形矢量(mm)
Fig.7
Deformation vector of coal pillar at -10 ℃ at different deformation stages (mm)
图8
图8
-4 ℃煤柱不同变形阶段的变形矢量(mm)
Fig.8
Deformation vector of coal pillar at -4 ℃ at different deformation stages (mm)
图9
图9
20 ℃煤柱不同变形阶段的变形矢量(mm)
Fig.9
Deformation vector of coal pillar at 20 ℃ at different deformation stages (mm)
3.3 弹性模量变化规律
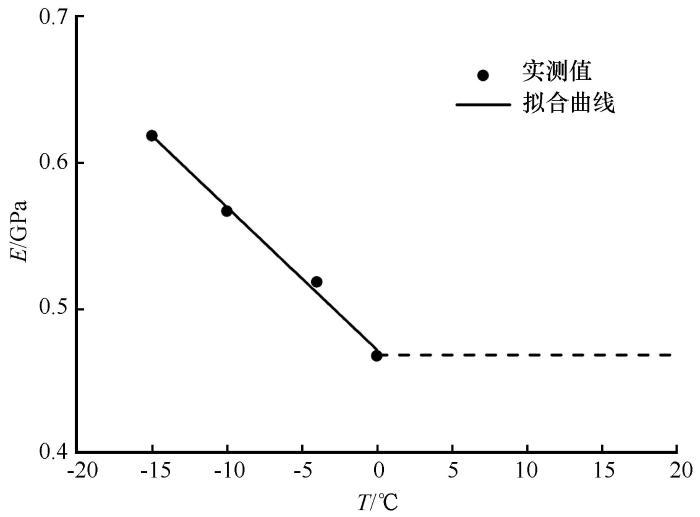
通过对四种温度下煤岩的单轴压缩数值试验, 可以得到煤岩在不同温度下的弹性模量.由数值试验结果可知, 煤岩的弹性模量随温度的降低而增加。出现这样的现象是因为随着温度的降低, 煤岩中未冻水转化成冰, 冰的胶结作用使得煤岩体克服了裂隙结构的缺陷, 整体性增强, 从而抵抗弹性变形的能力增强; 温度较高的煤岩体中含冰量少, 冰的胶结作用减弱, 从而使的煤岩的整体性下降, 抵抗弹性变形的能力有所减弱。对煤岩的弹性模量进行线性拟合, 可以得到如下结果, 如图10所示。
图10
图10
煤岩弹性模量与温度的关系
Fig.10
Relationship between elastic modulus and temperature of coal sample: measured and fitted
线性关系可以用如下关系式表示:
式中: E是煤岩弹性模量; E0是参考弹性模量, 取1 MPa; T是温度; T0是参考温度取-1
当温度为正温时, 煤岩体的弹性模量不再受温度的影响。
3.4 强度变化规律
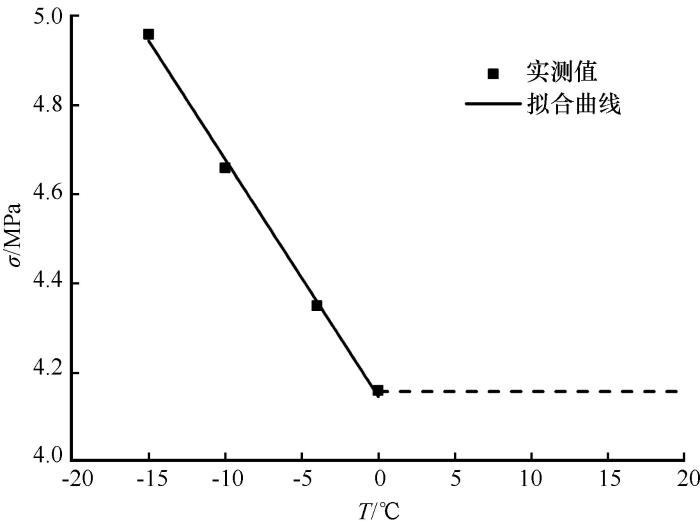
通过对四种温度下煤岩的单轴压缩数值试验, 可以得到煤岩在不同温度下的强度值。由数值试验结果可知, 煤岩的强度值随温度的降低而增大。出现这样的现象是因为随着温度的降低, 煤岩中的未冻水冻结成冰, 冰填充了煤岩的裂隙结构, 同时冰的胶结作用也使得在裂隙面相互接触的块体黏结增强, 从而煤岩的强度增加; 随着温度的升高, 煤岩中的冰含量减小, 冰对节理面上相互接触的块体黏结减弱, 在外载作用下, 煤岩中的软弱裂隙面出现缝隙或缝隙增大, 变形迅速发展从而破坏。对煤岩的强度进行拟合, 可以得到如下结果(图11)。
图11
图11
煤岩单轴抗压强度与温度的关系
Fig.11
Relationship between uniaxial compressive strength and temperature of coal sample: measured and fitted
线性关系可以用如下关系式表示:
式中: σc 煤岩抗压强度; σ0是参考强度值, 取1 MPa; T是温度; T0是参考温度值, 取-1
当温度为正温时, 煤岩体的强度不再受温度的影响。
4 结论与讨论
采用本文的细观参数对冻结裂隙煤岩的单轴抗压强度试验进行三维离散元数值模拟, 通过对不同温度下煤岩的应力-应变曲线、 位移以及其力学参数进行分析, 可以得到以下结论:
(1) 在单轴压缩情况下, 由于室内试验煤柱存在天然缺陷, 加载后会发生接触压密过程, 因而试验初始阶段的数值模拟曲线与试验应力-应变关系有一定的偏差, 但随着煤柱的完全压密, 偏差越来越小, 离散元模拟曲线总体上能反映冻结裂隙煤岩的压裂破坏过程。
(2) 在弹性压缩阶段, 煤岩内的位移呈层状分布, 且变形量较小; 屈服后的煤岩将从节理面发生滑移, 煤岩的变形急剧增加, 并且水平位移稍大于竖向位移, 煤柱表面将由表及里逐渐发生剥离破坏。
(3) 随着冻结温度的降低, 煤岩的弹性模量、 强度呈线性规律增加; 但温度变化不会改变煤岩的破坏形式。
本文应用力学试验和数值模拟相结合的研究手段, 揭示了冻结裂隙煤岩细观结构损伤演化与宏观力学变形过程之间的定性关系, 为从微观损伤角度研究岩体工程的安全稳定奠定了理论基础和技术储备。但鉴于自然裂隙岩体的多变性和复杂性, 本文仍然存在以下问题:
(1) 采用了传统的Mohr-Coulomb强度理论来分析, 而Mohr-Coulomb强度理论将剪切滑移面理想为平直面, 只是涉及了煤岩介质在平面情况下的摩擦系数, 忽略了实际情况下岩体断裂面极为粗糙的现象和本质。
(2) 基于煤样CT扫描获得了裂隙/节理几何尺寸和分布状态, 以此采用节理随机生成方法建立了裂隙煤岩的数值模型。但受CT扫描技术和图像处理技术所限, 不能获取煤样真实的裂隙/节理分布状况, 因此, 急需研发高精度、 大尺度岩体三维扫描技术, 以便获取准确的岩体细观结构状态。
(3) 由于冻结裂隙煤岩中冰的存在, 使得煤岩内部的接触、 冰对煤岩的胶结作用等更加复杂, 这都导致了模拟值与真实值之间存在一定的偏差。因此, 需要优化接触模型, 并且还需考虑冻结煤岩中冰的胶结作用, 建立煤岩细观参数与宏观响应之间的关系, 从而精确解释冻结裂隙煤岩的损伤破坏机理及力学性质。
参考文献
Numerical simulation of porous rock damage and failure
[J].
孔隙煤岩损伤破坏行为的数值模拟
[J].
Development and prospect of research on application of artificial ground freezing
[J].
人工地层冻结应用研究进展和展望
[J].
Testing frame design and research of temperature field of frozen artificial ground
[J].
人工地层冻结温度场试验台设计和研究
[J].
Study on the energy dynamic balance on coal and gas outburst
[J].
煤与瓦斯突出过程中能量动态平衡
[J].
Research on feasibility in preventing the coal and gas outburst by infecting liquid and freezing in uncovering coal seam in cross-cut
[J].
注液冻结法在石门揭煤中防突作用的可行性研究
[J].
Critical problems of freeze-thaw damage in fractured rock and their research status
[J].
裂隙岩体冻融损伤关键问题及研究状况
[J].
Advance and review on freezing-thawing damage of fractured rock
[J].
裂隙岩体冻融损伤研究进展与思考
[J].
Analysis of unfrozen water content and damage characteristics based on histogram technique of CT images
[J].
基于CT图像直方图技术的冻结岩石未冻水含量及损伤特性分析
[J].
A research on sandstone uniaxial and triaxial compression tests
[J].
砂岩单轴三轴压缩试验研究
[J].
Coupled evolution of damage and porosity in poroelastic media theory and applications to deformation of porous rocks
[J].
Study on rock strength characteristics based on uniaxial compression tests
[J].
岩石强度特性的单轴压缩试验研究
[J].
Statistical constitutive model for rock damage under uniaxial compression and its experimental study
[J].
单轴压缩下岩石损伤统计本构模型与试验研究
[J].
Experimental study on meso-damage evolution of coal under uniaxial compression
[J].
压缩荷载下煤岩损伤演化规律细观实验研究
[J].
Micro and meso-damage mechanism of coal’s strength and deformation characteristics
[J].
煤岩强度及变形特征的微细观损伤机理
[J].
Numerical simulation to outburst mechanism of coal or rock contain gas with FRPA2D system
[J].
含瓦斯“试样”突出现象的RFPA2D数值模拟
[J].
3D Numerical simulation of failure process of rock
[J].
岩石三维破裂过程的数值模拟研究
[J].
Numerical analysis of rock joint failure under compression-shear stress
[J].
岩石节理压剪破坏的数值分析
[J].
Researchon the shearing strength of rock joint
[J].
岩石节理剪切强度研究
[J].
Numerical simulation of zonal disintegration for deep rock mass
[J].
深部岩体分区破裂化现象数值模拟
[J].
Study of numerical simulation method of rock fracture based on strain energy density theory
[J].
基于应变能密度理论的岩石破裂数值模拟方法研究
[J].
Numerical simulation for energy mechanism of underground dynamic disaster
[J].
煤岩动力灾害能量机理的数值模拟
[J].


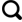








 甘公网安备 62010202000676号
甘公网安备 62010202000676号