0 引言
活动层厚度的现场测量主要有钻孔、触探、挖探等机械方法以及监测站监测等方法。Hon等[6]利用动态圆锥贯入仪在活动层与多年冻土层的动力锥穿透指数的不同,从而测定活动层厚度。更多学者则是通过不同地区的现场测量数据对活动层厚度的年际变化进行研究分析[7-9],Zhao等[10]根据青藏高原钻孔温度曲线证明,在1967—1997年期间,其活动层的厚度以平均速度为0.71 cm·a-1增长。Wu等[11]通过对青藏公路沿线监测站监测数据分析研究,发现从1995—2007年期间,青藏高原多年冻土区活动层厚度正以平均7.5 cm·a-1的速率持续增加。活动层厚度现场测量虽然能够获得较高的精确度,但存在着成本高、数据样本少且难以连续观测致使其无法刻画大区域特征等缺点。
针对以上不足,许多学者发现经验公式模型、统计模型和数值模型对活动层厚度大区域分布研究具有较好的效果。Pang等[12-13]用Stefan和Kudryavtsev公式计算了青藏高原活动层厚度的变化,给出了青藏高原活动层厚度空间分布图并预测了2049年、2099年的活动层厚度变化情况。Zhao等[14]将Kudryavtsev公式与Lund-Postam-Jena模型[15-16]耦合进一步提高了经验公式模型对活动层厚度的预测能力。Ni等[17]采用统计模型与机器学习结合的方式对青藏高原活动层厚度进行预测,研究发现模型比以往的研究具有较高的精度。Zhang等[18]利用改进的GIPL2模型对青藏高原无人区活动层厚度进行数值模拟,并基于实测活动层厚度数据验证了数值模型的准确性和优越性。总体而言,经验公式、统计模型和数值模型能够有效的描绘大区域活动层厚度分布情况,但对局地因素考虑不全且未能结合实地勘查数据进行研究,致使空间分辨率低,难以反映实际情况。
1 数据与研究方法
1.1 研究区概况
青藏工程走廊始于格尔木,止于拉萨市,横穿青藏高原1 120多公里,穿越多年冻土区约550 km,是内陆进入西藏的重要通道。本文以走廊内多年冻土区段(西大滩—安多)为研究区,研究活动层厚度分布状况。如图1所示,研究区以青藏公路、青藏铁路为基准线向两侧外延10 km,全长约540 km,地理坐标位于32°~36° N、91°~95° E,海拔介于3 716~6 191 m,该区地貌类型丰富,包括中高山区、高平原、低山丘陵、河谷等。
图1
1.2 数据源
活动层是地-气间水热交换的主要场所,大的气候背景决定了大区域活动层厚度的宏观分布状况。但在一定条件下,局地因素的影响将超过气候的影响,导致区域内相同气候背景下活动层厚度的分布异常。局地因素主要通过影响太阳辐射、热对流和热传导等过程从而影响活动层厚度的大小。因此,本文拟选用年平均地表温度、平均植被指数、纬度、高程、等效纬度和含冰量六类数据作为预测模型建立的预测因子。
年平均地表温度、平均植被指数和高程遥感数据由美国国家航天航空局下载的地表温度(MOD11A2 H25V05,2000—2016年)、植被指数(MOD13Q1 H25V05,2000—2016年)和SRTM-DEM(Shuttle Radar Topography Mission-Digital Elevation Model)数据产品中提取。等效纬度是表征太阳辐射对地表的影响,也是判断坡面走向的重要数据,可通过由SRTM-DEM数据产品中提取的坡度、坡向和纬度数据计算得到:
式中:
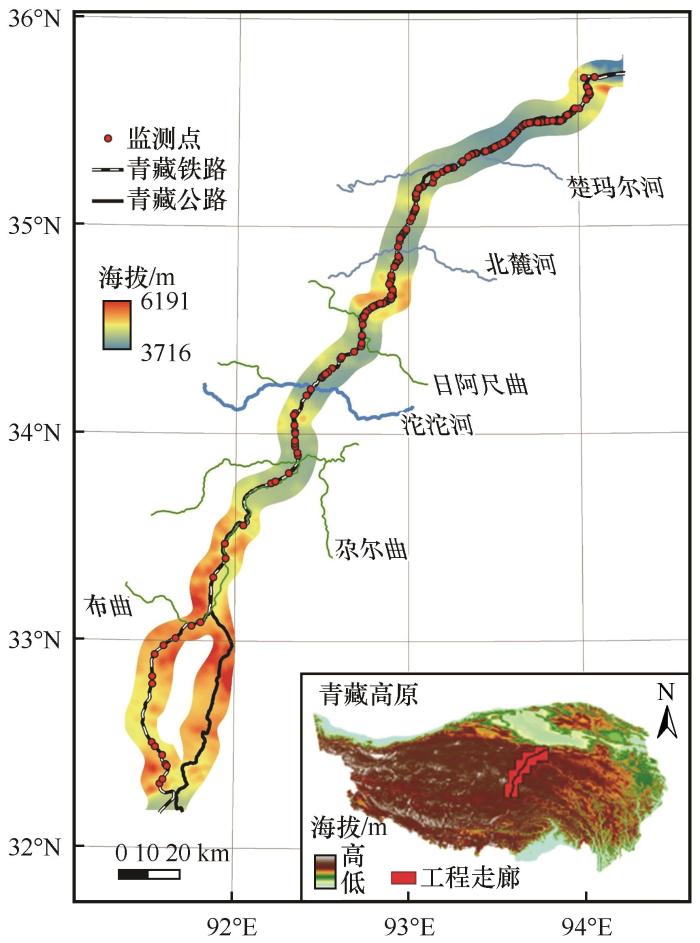
冻土含冰量是多年冻土的基本特征指标之一,且活动层内不同含冰量也对活动层热量吸收能力有一定影响。含冰量数据由现场钻取多年冻土上限以下8 m深度内的土层,再经过现场观察记录和室内试验综合确定。冻土含冰量钻孔点沿青藏铁路和青藏公路间隔2 km布置,确定所有钻孔点含冰量赋存状态后,再利用概率插值得到走廊带内冻土含冰量分布,如图2所示。目前,含冰量分类标准主要以《冻土工程地质勘察规范》(50324—2014)为主[24],分为少冰、多冰、富冰、饱冰和含土冰层五类。但在青藏高原地区,多年冻土上限以下土层内含冰量变化较为剧烈。因此,本文将根据多年冻土上限以下8 m深度内土层含冰量主要的赋存类型将含冰量划分为少冰-多冰、多冰-富冰、富冰-饱冰、饱冰-含土冰层四类。
图2
用于建立预测模型的活动层厚度实测数据来源于青藏公路、青藏铁路沿线监测断面地温监测数据(监测点如图1),监测工作由中交第一公路勘察设计研究院有限公司高寒高海拔地区道路工程安全与健康国家重点实验室格尔木观测基地完成,数据时限为2006—2016年,数据采集采用测温法测得,精度为±0.05 ℃。活动层厚度监测点共计300组,在研究区内分布较为平均,基本体现了青藏高原工程走廊带活动层厚度特征,具有较好的代表性。
1.3 预测因子间相关性分析
表1是各预测因子之间的相关性分析及共线性分析结果。由表可知,部分预测因子间虽然表现出较显著的相关性,但线性相关关系较弱,说明各预测因子间虽然能够相互影响,但影响程度较小。并且从共线性分析可以看出,各预测因子与活动层厚度之间的容差皆大于0.2且膨胀方差因子(VIF)皆小于5,这进一步说明各预测因子之间不存在明显的共线性。
表1 各因子之间的相关性及共线性分析
Table 1
| 因子 | 年平均地表温度 | 平均植被指数 | 等效纬度 | 纬度 | 高程 | 含冰量 | 共线性统计量 | |
|---|---|---|---|---|---|---|---|---|
| 容差 | VIF | |||||||
| 年平均地表温度 | 1 | — | — | — | — | — | 0.309 | 3.232 |
| 平均植被指数 | 0.003 | 1 | — | — | — | — | 0.626 | 1.597 |
| 等效纬度 | -0.243** | 0.189** | 1 | — | — | — | 0.293 | 3.413 |
| 纬度 | -0.342** | -0.548** | 0.050 | 1 | — | — | 0.298 | 3.359 |
| 高程 | -0.436** | 0.406** | -0.039 | -0.500** | 1 | — | 0.806 | 1.240 |
| 含冰量 | -0.360** | -0.006 | 0.071 | 0.139* | 0.112 | 1 | 0.865 | 1.156 |
1.4 研究方法
1.4.1 经验公式
最小二乘法是通过找寻数据误差平方和的最小值,从而确定数据的最佳匹配函数。在本文中,含冰量数据作为分类变量,因此,在进行经验公式拟合之前需对含冰量数据进行编码处理。目前,对于分类变量的编码方式主要有独热编码、虚拟编码和效应编码等。其中,效应编码具有不冗余、易于解释的优点,其原理是在一个具有n个类别的变量中选取一个类别作为参照(赋值为-1),从而创建n-1个指标变量(赋值为0或1)。含冰量数据编码处理方法如表2所示。
表2 含冰量数据效应编码
Table 2
| 含冰量 | 效应编码 | ||
|---|---|---|---|
| X1 | X2 | X3 | |
| 少冰-多冰 | -1 | -1 | -1 |
| 多冰-富冰 | 1 | 0 | 0 |
| 富冰-饱冰 | 0 | 1 | 0 |
| 饱冰-含土冰层 | 0 | 0 | 1 |
以上编码代表当含冰量为少冰-多冰时,X1、X2、X3取值为-1、-1、-1;含冰量为多冰-富冰时,X1、X2、X3取值为1、0、0,以此类推。因此基于最小二乘法拟合的活动层厚度经验公式如
式中:h为活动层厚度;Ts为年平均地表温度;N为平均植被指数;φ为纬度;H为高程;
1.4.2 机器学习
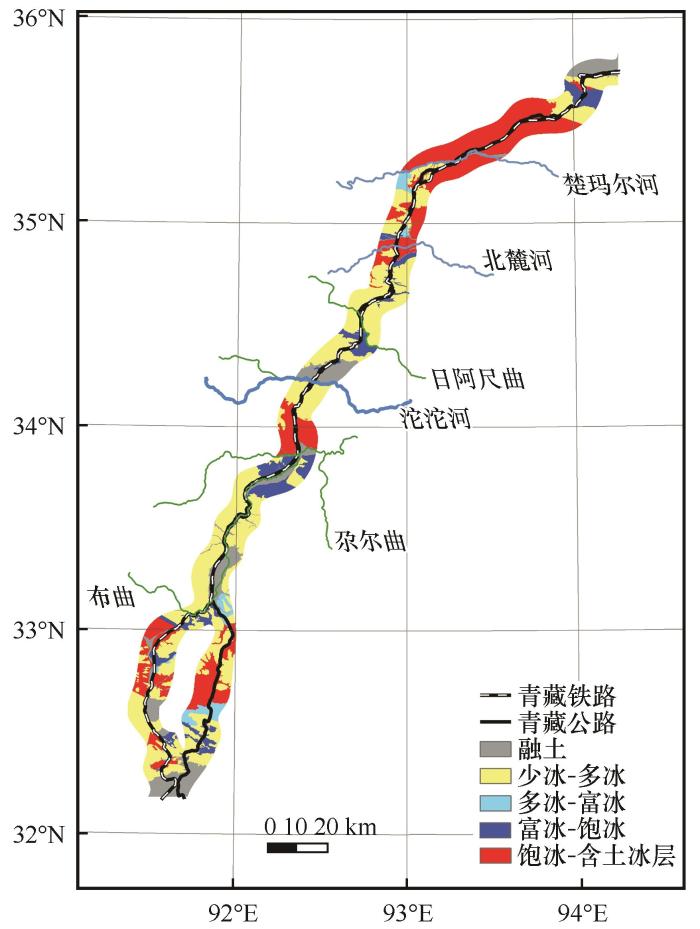
图3
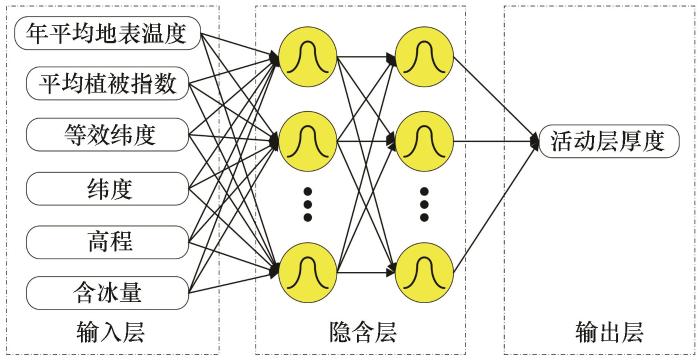
RBF神经网络是三层前馈神经网络,由输入层、隐含层和输出层三部分构成。其中,输入层用于接收外部信息,隐含层实现参数间的非线性转换,输出层用于输出最终结果,其结构如图4所示。k-fold交叉验证法是一种能够有效的利用小样本数据得到最优模型的方法。其原理是将原始数据分成k组,将每一组数据分别做一次验证集,其余的 k-1组数据作为训练集,从而得到k个模型,最终选择最优的模型。本文的RBF神经网络模型的结构设置为年平均地表温度、平均植被指数、等效纬度、纬度、高程和含冰量作为输入层,活动层厚度作为输出层,高斯径向基函数为激活函数。隐含层设置为两层,每层12个节点。k-fold交叉验证数为5,其中4份用于模型训练,1份用于模型验证,模型训练和模型验证样本数分别为240和60。
图4
1.4.3 评价指标
活动层厚度预测模型评价指标采用决定系数(R-Squared, R2)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、均方根误差(Root Mean Square Error, RMSE)和相对误差±15%内占比。其中R2、MAPE、RMSE表达式分别见式(
式中:
2 结果与讨论
2.1 模型结果对比
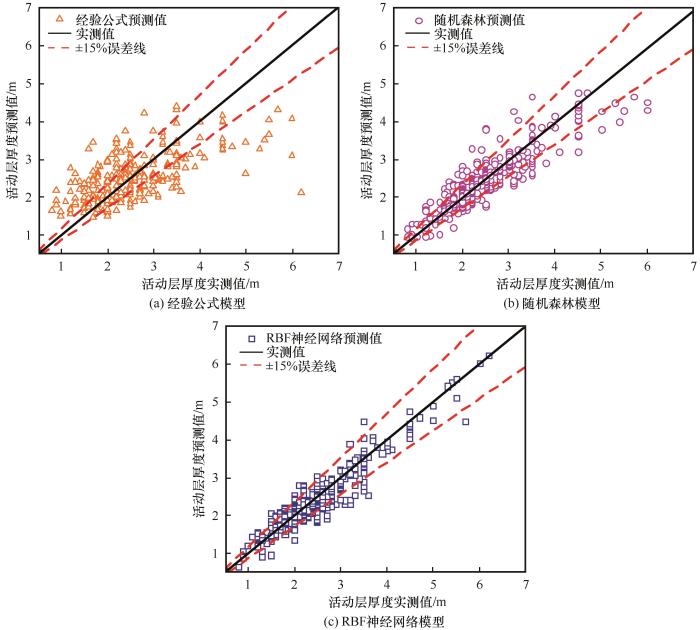
图5为三种活动层厚度预测模型的预测结果。由图可知,经验公式方法拟合效果最差,预测值大部分都分布于±15%误差线外,并且可以发现在低活动层厚度区间预测值偏大,高活动层厚度区间预测值偏小,整体分布极为离散。随机森林方法拟合效果次之,预测值大部分落在±15%误差线内。但整体来看,样本点仍较为离散,部分测点偏离实测值较大。说明随机森林方法虽然能够较好的预测活动层厚度,但存在一定误差。RBF神经网络方法拟合效果最好,预测值基本位于±15%误差线内,并且整体更靠近实测值线,尤其高活动层厚度区间。因此,从三种方法预测结果对比可知,基于RBF神经网络方法的活动层厚度预测模型预测效果最为精确、稳定。
图5
图5
各活动层厚度预测模型结果对比
Fig.5
Comparison of results of prediction models for the thickness of each active layer
表3为三种预测模型的各项评价指标。由表可知,经验公式预测模型的各项评价指标的评价优度均较差,R2仅为0.40,RMSE和MAPE达到0.75和24.5%,相对误差在±15%以内的占比也不足一半。随机森林和RBF神经网络预测模型的R2、RMSE、MAPE、相对误差在±15%内占比分别为0.72和0.84、0.42和0.32、12.7%和10.5%、69.6%和74.6%。与经验公式预测模型相比,各项评价指标的评价优度有较大提升。说明机器学习方法对活动层厚度的预测更加准确、误差更小。且可以看出RBF神经网络预测模型的各项评价指标评价优度均好于随机森林预测模型。说明RBF神经网络方法在处理非线性关系、捕捉各活动层厚度拟合参数之间的特征联系以及全局逼近和逼近精度都好于随机森林方法。
表3 三种预测模型的各项评价指标
Table 3
| 预测模型 | 评价指标 | |||
|---|---|---|---|---|
| R2 | RMSE | MAPE | 相对误差 ±15%内占比 | |
| 经验公式 | 0.40 | 0.75 | 24.5% | 41.0% |
| 随机森林 | 0.72 | 0.42 | 12.7% | 69.6% |
| RBF神经网络 | 0.84 | 0.32 | 10.5% | 74.6% |
2.2 敏感性分析
由以上三种预测模型的预测结果对比可知RBF神经网络模型为预测活动层厚度的最佳模型,因此选择对RBF神经网络模型的预测结果进行敏感性分析。敏感性分析是研究输入参数的变化对输出结果的影响程度。Sabol方法[30]是一种全局敏感性分析方法,能够有效的处理非线性响应和度量非加性系统中相互作用的影响。其计算公式如下:
式中:STi为总效应指数,表示敏感性程度大小;Var表示方差;E表示期望;Y表示输出变量;Xi代表输入因子;X~i表示除Xi所有变量的集合。计算结果如表4所示,由表可知,含冰量对于活动层厚度的影响性最大,其次为年平均地表温度、高程、等效纬度、纬度和平均植被指数。
表4 各预测因子敏感性分析
Table 4
| 预测因子 | 年平均地表温度 | 平均植被指数 | 纬度 | 高程 | 等效纬度 | 含冰量 |
|---|---|---|---|---|---|---|
| STi | 0.609 | 0.389 | 0.454 | 0.563 | 0.488 | 0.705 |
| 敏感性排序 | 2 | 6 | 5 | 3 | 4 | 1 |
2.3 以往文献结果对比
表5为以往学者对活动层厚度预测模型和本文RBF神经网络预测模型的评价指标对比。由表可知,本文以RBF神经网络建立的活动层厚度预测模型的预测效果好于以往的研究成果,R2和RMSE的提升幅度较为明显。此外,可以发现文献中经验公式预测方法的预测效果并不理想,而采用机器学习方法后,预测效果得到极大的改善,这进一步说明活动层厚度与各预测因子之间具有极强的非线性关系。从预测因子来看,本文与以往文献相比除了温度、植被、地形等因子,还考虑了含冰量的影响。由表可知,未考虑含冰量参数的RBF神经网络预测模型的R2和RMSE分别为0.71和0.43,与以往的机器学习方法研究结果精度相当。而考虑含冰量参数的RBF神经网络预测模型R2和RMSE分别为0.84和0.32,预测效果明显提升,说明含冰量是活动层厚度的重要影响因素之一。
表5 不同活动层厚度预测模型的对比
Table 5
3 活动层厚度分布
通过以上模型的对比分析,最终确定以RBF神经网络作为预测方法建立活动层厚度预测模型。本文采用ArcGIS 10.5软件绘制活动层厚度分布图,具体步骤为:(1)对年平均地表温度、平均植被指数、等效纬度、高程和含冰量数据的栅格图进行点数据提取,纬度数据由ArcGIS软件计算得到;(2)将点数据输入至RBF神经网络活动层厚度预测模型中,求取各点的活动层厚度;(3)将各点活动层厚度导入至ArcGIS中,为使图层精度提高、平滑性增强,采用克里金插值法进行制图,即可获得研究区内多年冻土活动层厚度分布区划图。
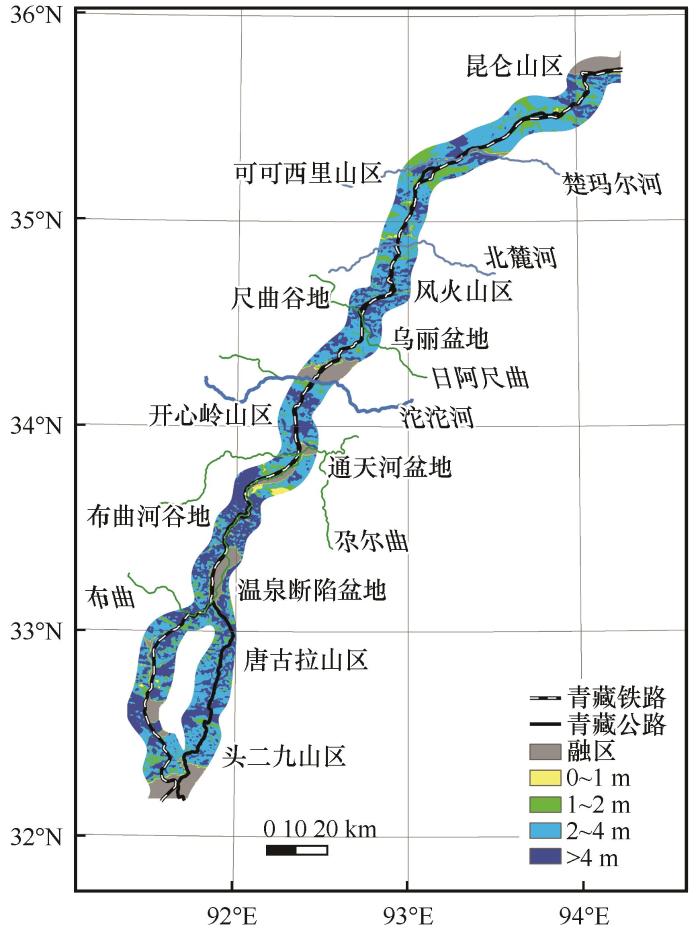
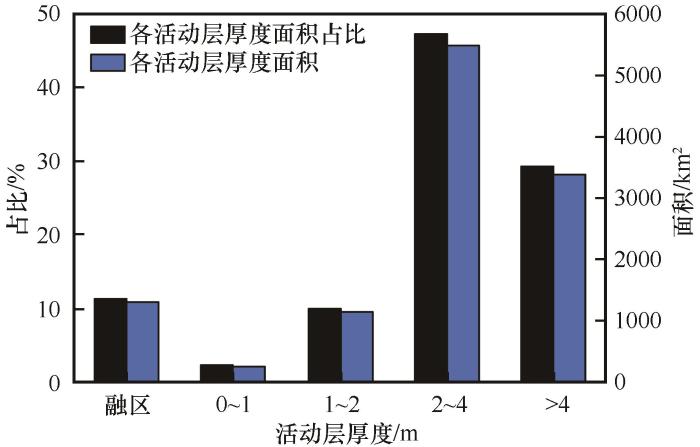
图6为青藏工程走廊活动层厚度分布区划图。由以上步骤(2)中的预测模型计算结果可知,研究区活动层厚度分布范围在0.60~6.30 m,平均活动层厚度为3.55 m。图7为研究区各活动层厚度面积与面积占比。结合图6可知,研究区内活动层厚度主要为2~4 m,总面积为5 468.3 km2,面积占比为47.27%,主要分布于楚玛尔平原至北麓河盆地和唐古拉山区南部至头二九山区;活动层厚度大于4 m次之,总面积为3 382.3 km2,面积占比为29.24%,整体分布偏向南部地区,主要分布于布曲河谷地至头二九山区;活动层厚度为0~2 m在研究区分布较少,面积占比仅达到12.2%,在研究区内分布较零散,主要分布于楚玛尔河平原和可可西里山区。
图6
图7
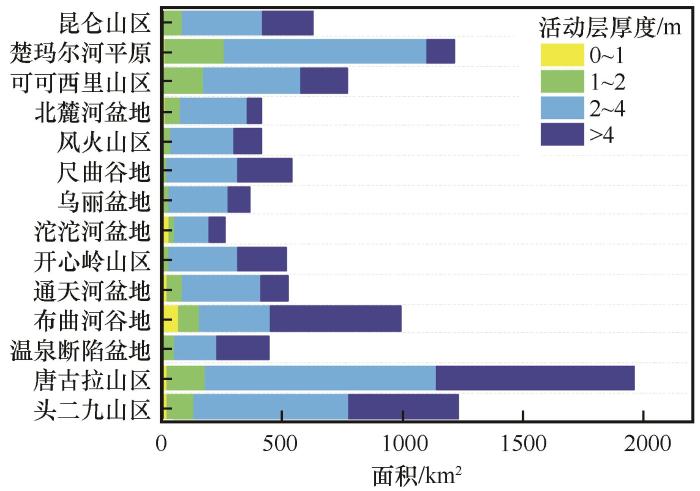
各区域不同活动层厚度面积如图8所示。由图可知,昆仑山区至北麓河盆地的活动层厚度主要在1 m以上,整个青藏工程走廊内活动层厚度为1~2 m区域主要分布于此区段。活动层厚度为2~4 m的区域也在此区段内占有较大面积比例,如楚玛尔河平原和北麓河盆地的面积占比达到69.16%和68.52%。风火山区至开心岭山区的活动层厚度主要在2 m以上,且此区段各区域内活动层厚度主要为2~4 m。其中,尺曲谷地和开心岭山区活动层厚度大于4 m的也占有较大面积。通天河盆地至头二九山区的活动层厚度主要以2~4 m和4 m以上的情况居多,主要分布于布曲河谷地、唐古拉山和头二九山地区。
图8
图8
各区域不同活动层厚度面积
Fig.8
Areas of different active layer thicknesses in each region
4 活动层厚度与含冰量、地温关系
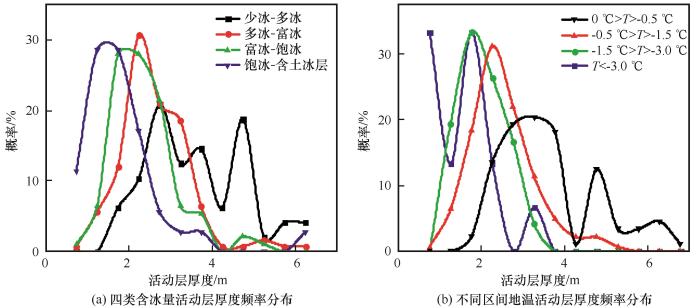
为探究研究区活动层厚度与含冰量和地温的关系,对研究区四类含冰量和不同区间的地温的活动层厚度数据进行统计,得到其概率分布如图9所示。由图9(a)可知,四类含冰量的活动层厚度主要分布区间(分布概率大于10%)为2.21~4.00 m与4.42~5.03 m、1.62~3.60 m、1.33~3.10 m和0.75~2.52 m,均值为3.48 m、2.55 m、2.28 m和1.78 m。四类含冰量活动层厚度概率曲线随着含冰量增加,分布明显左偏,说明活动层厚度随着土层含冰量增加而减小。由图9(b)可知,不同区间的地温的活动层厚度主要分布区间(分布概率大于10%)为2.08~3.97 m与4.62~4.94 m、1.42~3.34 m、1.00~ 3.00 m和0.75~2.34 m,均值为3.44 m、2.41 m、1.92 m和1.48 m,即随着地温温度升高,活动层厚度增加。这是由于活动层的地温较低时,活动层内含冰量会相应的增加,而当外界温度变化时,具有高含冰量的活动层内将会发生着大量的冰-水相变过程,从而导致活动层升温速率过慢,致使活动层厚度较浅。
图9
图9
不同含冰量、地温的活动层厚度频率分布
Fig.9
Frequency distribution of active layer thickness with different ice content and ground temperature
5 结论
通过利用青藏工程走廊监测断面实测数据建立活动层厚度预测模型,再结合高精度遥感数据绘制青藏工程走廊多年冻土区的活动层厚度分布图,得出以下结论:
(1)经验公式、随机森林和RBF神经网络预测模型的预测效果对比可知,基于RBF神经网络方法的活动层厚度预测模型预测效果最为精确、稳定,其预测值基本位于±15%误差线内,且活动层厚度较大区间预测结果更接近实测值。
(2)考虑含冰量参数的RBF神经网络预测模型R2和RMSE分别为0.84和0.32,预测效果明显提升,说明含冰量是活动层厚度的重要影响因素之一。
(3)研究区内活动层厚度主要为2~4 m,总面积为5 468.3 km2,面积占比为47.27%,主要分布于楚玛尔平原至北麓河盆地和唐古拉山区南部至头二九山区;活动层厚度大于4 m次之,总面积为 3 382.3 km2,面积占比为29.24%,整体分布偏向南部地区,主要分布于布曲河谷地至头二九山区;活动层厚度为0~2 m在研究区分布较少,面积占比仅达到12.2%,在研究区内分布较零散。
(4)活动层厚度随含冰量增加而减小、随地温升高而增加,四类含冰量的活动层厚度主要分布区间为2.21~4.00 m与4.42~5.03 m、1.62~3.60 m、1.33~3.10 m和0.75~2.52 m,均值为3.48 m、 2.55 m、2.28 m和1.78 m。
参考文献
Third pole environment (TPE)
[J].
Recent permafrost warming on the Qinghai-Tibetan Plateau
[J].
Permafrost changes in the northern limit of permafrost on the Qinghai-Tibet Plateau in the last 30 years
[J].
近30年来青藏高原西大滩多年冻土变化
[J].
Processes and modes of permafrost degradation on the Qinghai-Tibet Plateau
[J].
青藏高原多年冻土退化过程及方式
[J].
Simulated distribution of active layer depths in the frozen ground regions of Tibetan Plateau
[J].
青藏高原冻土区活动层厚度分布模拟
[J].
Evaluation of active layer depth using dynamic cone penetrometer
[J].
Past and present permafrost temperatures in the Abisko area: Redrilling of boreholes
[J].
Recent changes in the active layer thickness across the Northern Hemisphere
[J].
Active layer monitoring at CALM-S site near J.G.Mendel Station, James Ross Island, eastern Antarctic Peninsula
[J].
Changes of climate and seasonally frozen ground over the past 30 years in Qinghai-Xizang (Tibetan) Plateau, China
[J].
Changes in active layer thickness over the Qinghai-Tibetan Plateau from 1995 to 2007
[J].
Active layer thickness calculation over the Qinghai-Tibet Plateau
[J].
Active layer thickness variations on the Qinghai-Tibet Plateau under the scenarios of climate change
[J].
Projected changes in permafrost active layer thickness over the Qinghai-Tibet Plateau under climate change
[J].
Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model
[J].
Terrestrial vegetation and water balance-hydrological evaluation of a dynamic global vegetation model
[J].
Simulation of the present and future projection of permafrost on the Qinghai-Tibet Plateau with statistical and machine learning models
[J].
Numerical modeling of the active layer thickness and permafrost thermal state across Qinghai-Tibetan Plateau
[J].
Data-driven mapping of the spatial distribution and potential changes of frozen ground over the Tibetan Plateau
[J].
Permafrost identification and annual mean ground temperatures prediction model for Qinghai-Tibet engineering corridor
[J].
青藏高原工程走廊带多年冻土辨识及年平均地温预估模型
[J].
Permafrost modeling and mapping along the Qinghai-Tibet engineering corridor considering slope-aspect
[J].
考虑局地因素坡向影响的青藏高原工程走廊冻土分布与制图研究
[J].
Mapping the permafrost stability on the Tibetan Plateau for 2005-2015
[J].
Machine learning-based thermokarst landslide susceptibility modeling across the permafrost region on the Qinghai-Tibet Plateau
[J].
Prediction model of summer land surface temperature in the Shiyang River basin based on the wavelet transform and neural network
[J].
基于小波变换与神经网络的石羊河流域夏季地温预测模型研究
[J].
Estimation of grassland net primary productivity in permafrost of Qinghai-Tibet Plateau based on machine learning
[J].
基于机器学习估算青藏高原多年冻土区草地净初级生产力
[J].
Research on experimental tests and prediction models of thermal conductivity of freezing-thawing soil in the Kunlun Mountains
[J].
昆仑山地区冻融土导热系数试验测试与预测模型研究
[J].
Sensitivity estimates for nonlinear mathematical models
[J].
Statistical forecasting of current and future circum-Arctic ground temperatures and active layer thickness
[J].


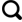



 甘公网安备 62010202000676号
甘公网安备 62010202000676号