Research progress of constitutive models of frozen soils: a review
1
2023
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
State-of-art of research on elastoplastic constitutive models of frozen soil
0
2019
Study on constitutive model of subgrade soil in seasonally frozen area
0
2023
Damage mechanism and dynamic constitutive model of frozen soil under uniaxial impact loading
0
2020
Effect of water content on yield surface of ice-rich frozen silty sand
0
2019
含水量对高含冰量冻结砂土屈服面的影响
0
2019
An elastoplastic model for saturated freezing soils based on thermo-poromechanics
1
2018
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Strength and creep of frozen soils and calculations in ice-soil retaining structures
1
1965
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Constitutive relations of frozen soil in uniaxial compression
1
1992
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
冻土的单轴压缩本构关系
1
1992
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Analyses of behavior of stress-strain of frozen Lanzhou loess subjected to K0 consolidation
1
2004
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
A damage constitutive model for frozen soils under uniaxial compression based on CT dynamic distinguishing
1
2005
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
基于动态CT识别的冻土单轴压缩损伤本构模型
1
2005
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Constitutive model of frozen soil with damage and numerical simulation of the coupled problem
1
2007
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
含损伤的冻土本构模型及耦合问题数值分析
1
2007
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Stress-strain relationships and nonlinear Mohr strength criterion of frozen sand clay
1
2007
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
冻结砂土的应力-应变关系及非线性莫尔强度准则
1
2007
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Laboratory and theoretical investigations on the deformation and strength behaviors of artificial frozen soil
1
2010
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Yield criterion and elasto-plastic damage constitutive model for frozen sandy soil
1
2009
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Strength criterion and elastoplastic constitutive model of frozen silt in generalized plastic mechanics
2
2010
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
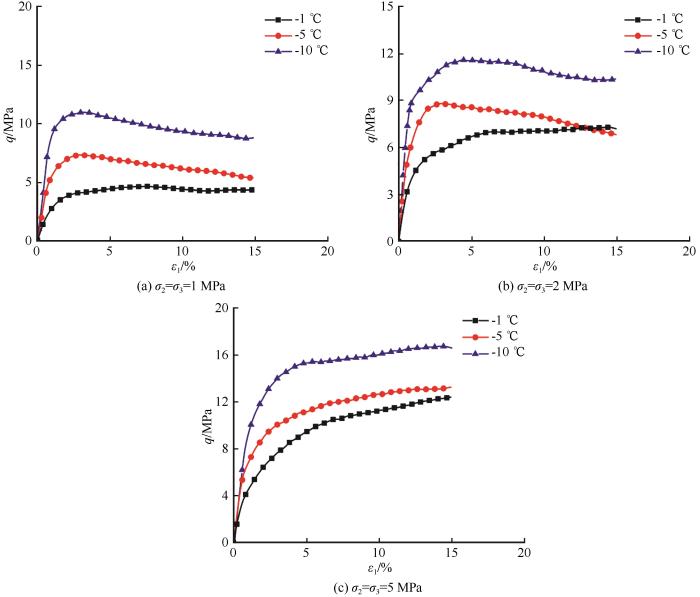
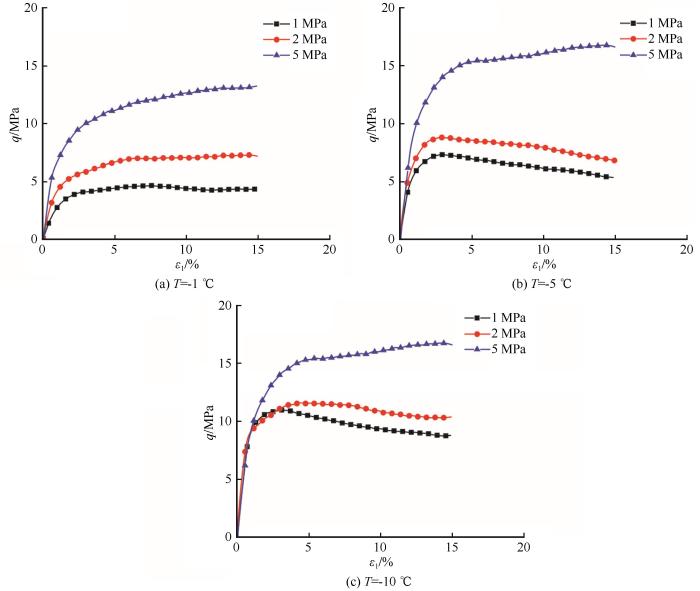
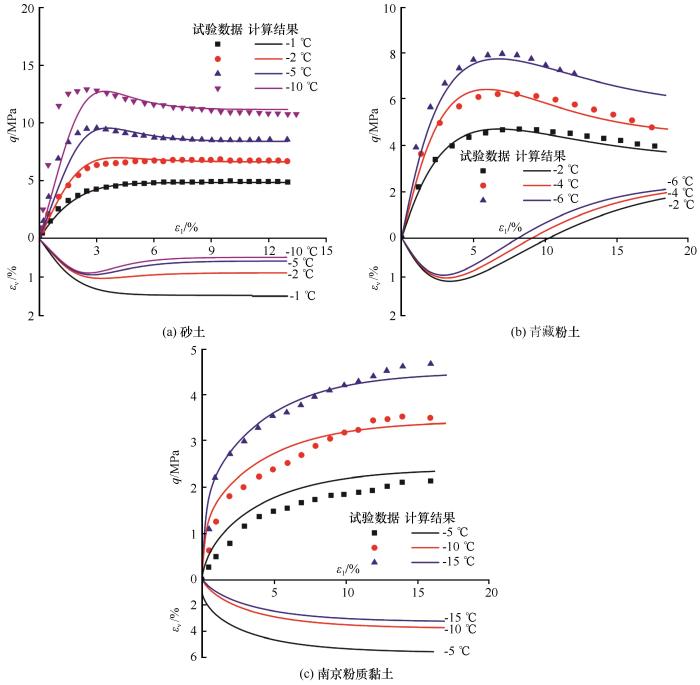
... Lai等[15]对青藏粉土、Xu等[21]对砂土、孙谷雨等[44]对南京粉质黏土在不同温度下进行了三轴剪切试验.使用表1参数对以上试验进行预测,试验数据与计算结果对比见图16.由于以上文献中没有提供体应变数据,因此仅给出了体应变的预测结果.图16(a)中,随着温度的降低,冻结砂土的应力-应变曲线由应变硬化型逐渐过渡为应变软化型,体应变曲线逐步由剪缩型过渡为剪胀型,这都表明冻土的表观超固结度随温度降低而增强.图16(b)中,冻结粉土的应力-应变曲线均为应变软化型,体应变曲线均为剪胀型,但应变软化程度和剪胀程度随着温度的降低而增强,也即表观超固结度随温度降低而增强.图16(c)中,应力-应变曲线均为应变硬化型,体应变曲线均为剪缩型,但随着温度降低,应力-应变曲线的峰值强度升高,体应变曲线的剪缩量减小.由以上各图可知,本文模型能够较好地反映温度对冻土应变软化程度和剪胀性的影响,也能较好描述冻土抗剪强度(包括峰值强度和残余强度)随温度降低而增大的规律. ...
A constitutive model of frozen saline sandy soil based on energy dissipation theory
1
2016
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Effect of temperature and strain rate on mechanical characteristics and constitutive model of frozen Helin loess
2
2017
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
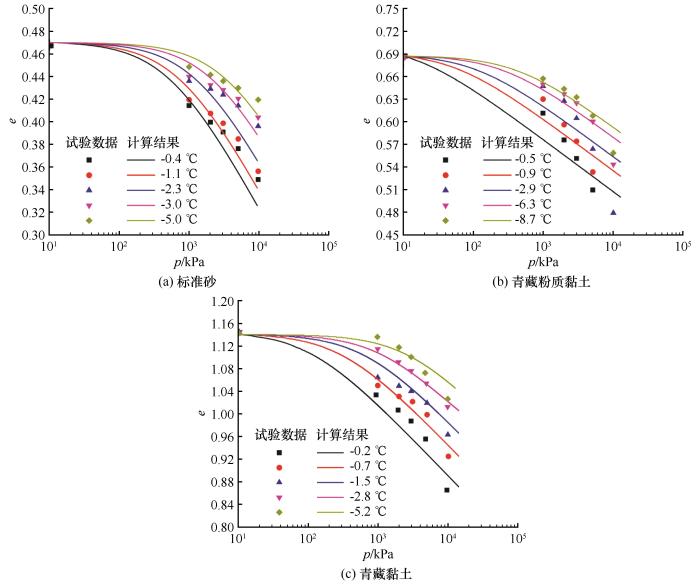
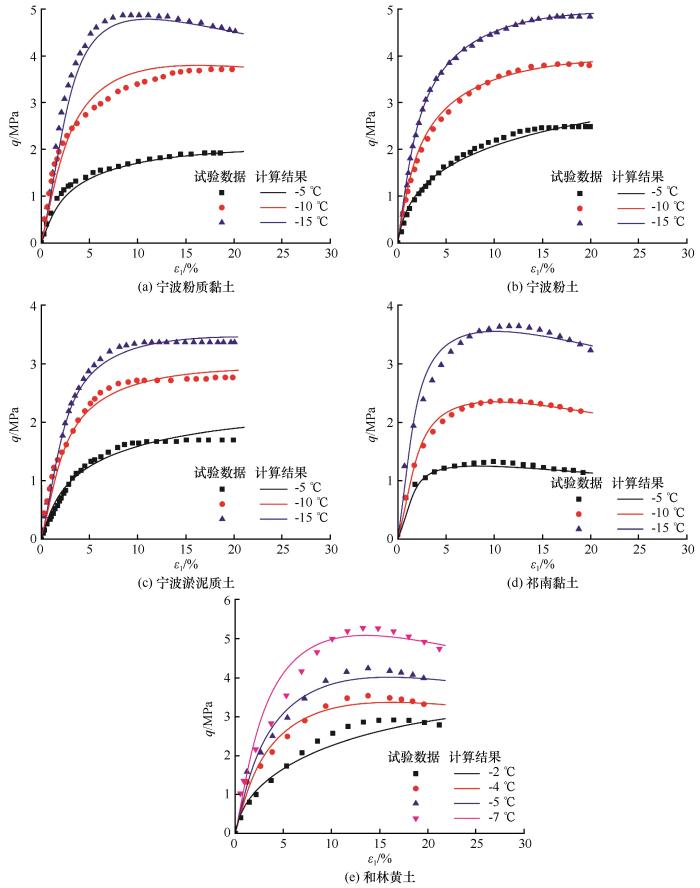
... 使用所提模型对文献中多种类型冻土的单轴压缩试验结果进行预测,包括宁波粉质黏土、粉土和淤泥质土[42]以及祁南黏土[43]、和林黄土[17],预测应力-应变曲线如图15所示.图中ε1为轴向应变,预测所用参数见表1.从图中可以看出,本文模型能够反映冻土单轴抗压强度随温度降低而升高的试验规律.并且,对于宁波粉质黏土、祁南黏土、和林黄土,其应力-应变曲线的应变软化程度随温度降低而增强,本文模型能够描述这一规律. ...
Binary-medium-based constitutive model of frozen soils subjected to triaxial loading
1
2019
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
An elastoplastic damage constitutive model for frozen soil based on the super/subloading yield surfaces
1
2020
... 鉴于冻土应力-应变关系对温度的高度敏感性,温度是建立冻土本构模型时所需要考虑的首要因素.自20世纪60年代开始,国内外学者分别基于非线性弹性理论、弹塑性理论、亚塑性理论、损伤理论、能量耗散理论以及二元介质理论建立了各种类型的冻土本构模型[1-6].例如,Vialov等[7]、朱元林等[8]、Wang等[9]采用非线性弹性理论建立了冻土本构模型;刘增利等[10]、宁建国等[11]在弹性应力-应变关系中引入损伤因子,建立了含损伤的冻土弹性本构模型;赖远明等[12]、Yang等[13]改进了抛物线形的非线性弹性应力-应变关系,使模型能够同时描述应变硬化和软化;Lai等[14]考虑了围压对冻土强度的影响,并将各向异性损伤因子与弹塑性框架结合,建立了冻结砂土的弹塑性本构模型;Lai等[15]扩展了Lade-Ducan三维强度准则,使其可以考虑压融的影响,将其与广义塑性理论结合,针对冻结粉土建立了可以描述应变硬化和软化的本构模型;Lai等[16]基于能量耗散理论从热力学角度出发针对冻结盐渍砂土建立了冻土弹塑性本构模型;Xu等[17]通过构建弹性模量、硬化参数等与温度和应变率的经验关系,在一般弹塑性力学的框架内针对和林黄土建立了本构模型;Zhang等[18]认为冻土由结构块和弱化带组成,并使用基于Ducan-Chang模型的摩擦单元来描述弱化带,从微观角度建立了冻土本构模型;Sun等[19]在上下加载面融土本构模型的基础上,一方面引入损伤因子描述冻土在受荷过程中的结构损伤,另一方面使用超固结参数来反映冰对冻土黏结强度的影响,建立了冻土的弹塑性本构模型.以上冻土本构模型已经能够较好地描述冻土在某一温度下的应力-应变关系.然而,以上这些模型在反映温度对冻土应力-应变关系的影响时,多采用直接修改模型参数或构建模型参数与温度之间经验关系的方法,所以难以模拟恒载变温和温载交变等复杂路径下的冻土力学行为,在应用到热水力耦合数值分析时受到限制. ...
Constitutive model of frozen soil
1
2014
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
冻土的本构关系
1
2014
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
An extended hypoplastic constitutive model for frozen sand
2
2016
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
... Lai等[15]对青藏粉土、Xu等[21]对砂土、孙谷雨等[44]对南京粉质黏土在不同温度下进行了三轴剪切试验.使用表1参数对以上试验进行预测,试验数据与计算结果对比见图16.由于以上文献中没有提供体应变数据,因此仅给出了体应变的预测结果.图16(a)中,随着温度的降低,冻结砂土的应力-应变曲线由应变硬化型逐渐过渡为应变软化型,体应变曲线逐步由剪缩型过渡为剪胀型,这都表明冻土的表观超固结度随温度降低而增强.图16(b)中,冻结粉土的应力-应变曲线均为应变软化型,体应变曲线均为剪胀型,但应变软化程度和剪胀程度随着温度的降低而增强,也即表观超固结度随温度降低而增强.图16(c)中,应力-应变曲线均为应变硬化型,体应变曲线均为剪缩型,但随着温度降低,应力-应变曲线的峰值强度升高,体应变曲线的剪缩量减小.由以上各图可知,本文模型能够较好地反映温度对冻土应变软化程度和剪胀性的影响,也能较好描述冻土抗剪强度(包括峰值强度和残余强度)随温度降低而增大的规律. ...
A simple framework for describing strength of saturated frozen soils as multi-phase coupled system
2
2019
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
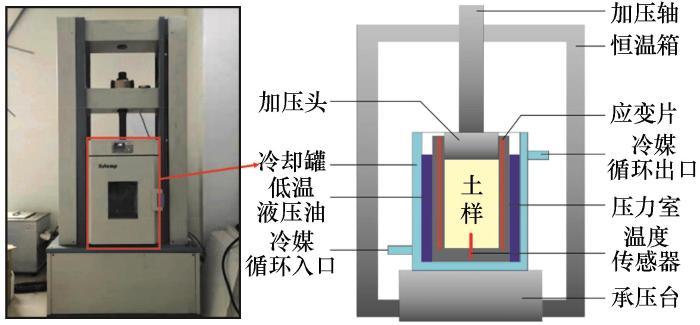
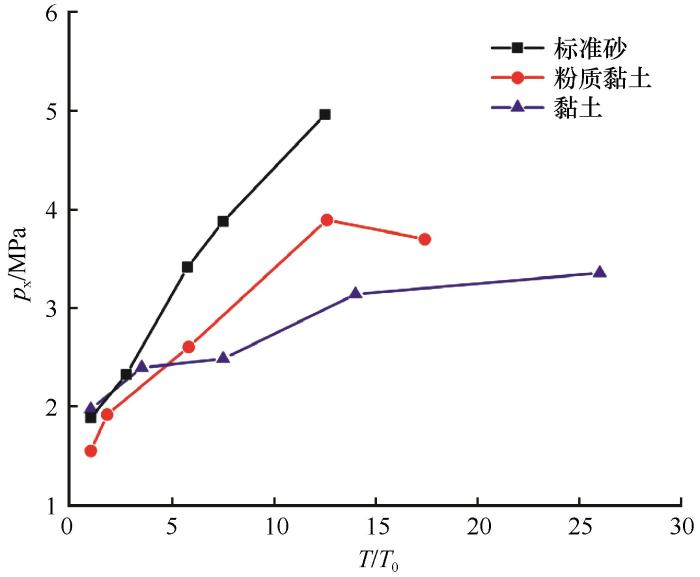
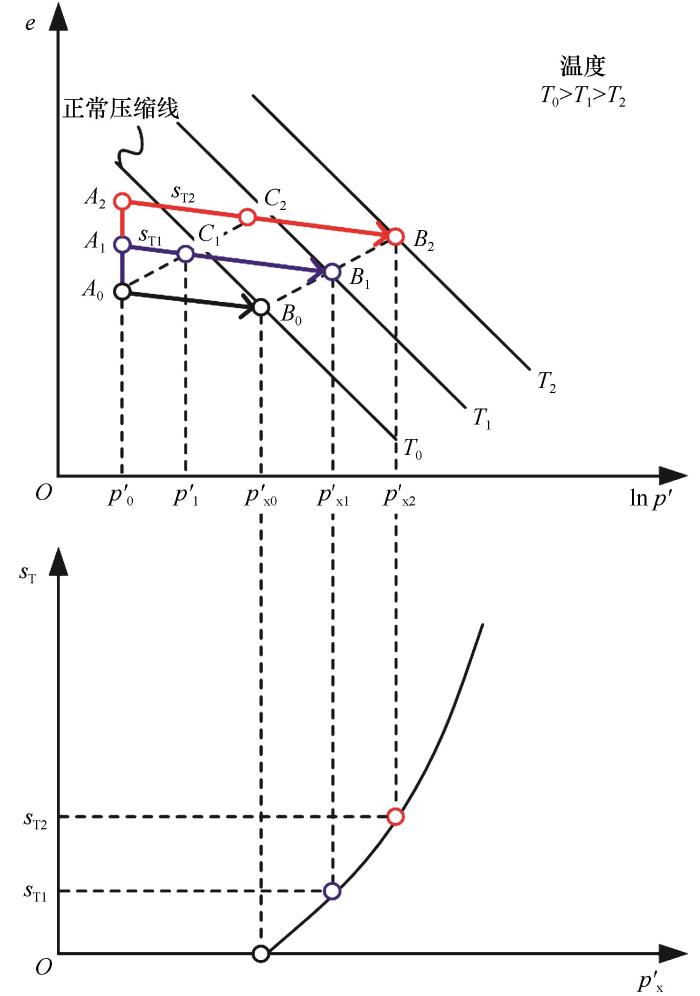
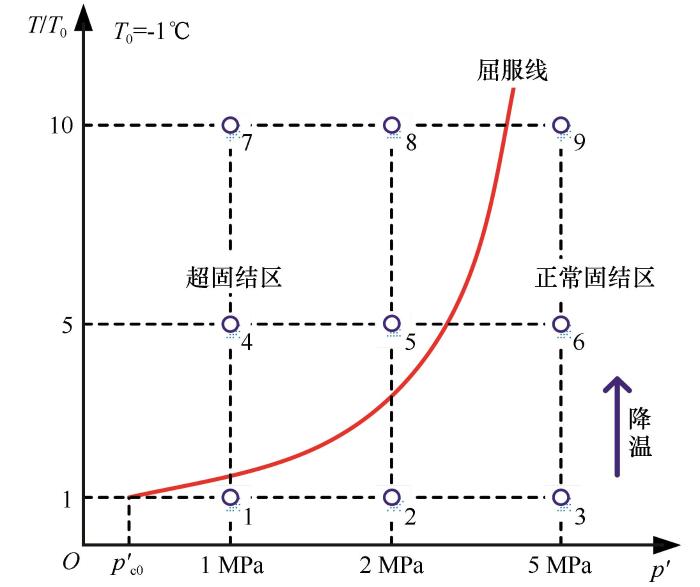
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
THM-coupled finite element analysis of frozen soil: formulation and application
4
2009
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
... 现有的冻土本构模型多以总应力为变量.以总应力为变量在建模环节以及与试验数据对比时有一定的便利性.然而,在寒区岩土工程热水力耦合分析等需要考虑融土和冻土相互转换的冻融循环工况中,采用总应力作为变量所建立的冻土本构模型难以退化到融土本构模型,从而影响这类工况的模拟分析[23].为了解决这一问题,冻土有效应力的概念被提出. ...
... 由于冻土内部冰-水-土相互作用的复杂性,目前冻土的有效应力理论尚不成熟,各研究中存在不同的有效应力表示方法.目前常用的有效应力表达方法有Bishop应力法[32]、净应力法[23]和固相应力法[33].Bishop应力法借鉴了非饱和土中Bishop应力的定义方式,采用下式计算冻土中的有效应力. ...
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
Discussion: a constitutive model for partially saturated soils
1
1991
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
Computational simulation of soil freezing: multiphase modeling and strength upscaling
1
2014
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
Thermal-hydro-mechanical analysis of frost heave and thaw settlement
1
2015
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
An elastic-viscoplastic model for saturated frozen soils
1
2022
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
A multisurface elastoplastic model for frozen soil
1
2021
... 近十几年来,部分学者尝试从温度影响冻土力学特性的机理出发,将温度作为变量直接引入冻土本构模型之中,以期可以预测热-水-力耦合条件下的冻土应力-应变关系.例如,罗小映等[20]根据冻土表观前期固结压力随温度变化的试验规律,认为温度对冻土力学特性产生影响的主要原因是改变了冻土的表观超固结度,从而基于超固结融土的统一硬化模型建立了冻土弹塑性本构模型;Xu等[21]认为温度主要影响冻土中冰对土颗粒的黏结强度,将黏结强度引入亚塑性理论,建立了冻土的亚塑性本构模型.以上关于温度对冻土力学特性影响的解释均停留在宏观层面,Nishimura等[22-23]则从微观角度出发,指出冻土中冰和未冻水之间存在压力差,这使得冻土内部产生类似于非饱和土基质吸力的低温吸力作用,从而基于Alonso等[24]提出的巴塞罗那非饱和融土本构模型建立了冻土的弹塑性本构模型.Zhou[25]、Zhang等[26]、Ghoreishian Amiri等[27]、Sun等[28]相继基于低温吸力理论建立了冻土本构模型.低温吸力冻土本构模型不仅在物理层面解释了温度对冻土力学特性产生影响的原因,而且在正温时可以退化到融土本构模型,实现了融土和冻土本构关系的统一,在应用于热水力耦合数值分析时具有一定优势.但是,一方面,目前低温吸力往往被解释为作用于冰-水界面的压力差,这与传统土力学中“影响土力学特性的应力为作用于土骨架上的有效应力”的认知不符;另一方面,根据低温吸力理论,低温吸力使冻土表现出一定的表观超固结性(apparent overconsolidation),而现有低温吸力冻土本构模型一般建立在正常固结融土本构模型的基础上,在描述应变软化和剪胀等现象时不尽完善. ...
The physics of premelted ice and its geophysical consequences
1
2006
... 受孔隙几何效应和土颗粒表面作用的影响,冻土内部始终存在一定数量的未冻水,未冻水即使在极低的温度下也依然存在.按照成因,冻土中的未冻水可分为两种类型:薄膜未冻水和毛细未冻水[29].如图1所示,薄膜未冻水因预熔作用形成,赋存在土颗粒表面,受土颗粒强烈的束缚作用.毛细未冻水因孔隙力学作用产生,赋存在孔隙之中.在黏土、粉质黏土和粉土等塑性较强的细粒土中,未冻水含量较为显著[30]. ...
Experimental study on the influence of specific surface area on the soil-freezing characteristic curve
1
2021
... 受孔隙几何效应和土颗粒表面作用的影响,冻土内部始终存在一定数量的未冻水,未冻水即使在极低的温度下也依然存在.按照成因,冻土中的未冻水可分为两种类型:薄膜未冻水和毛细未冻水[29].如图1所示,薄膜未冻水因预熔作用形成,赋存在土颗粒表面,受土颗粒强烈的束缚作用.毛细未冻水因孔隙力学作用产生,赋存在孔隙之中.在黏土、粉质黏土和粉土等塑性较强的细粒土中,未冻水含量较为显著[30]. ...
比表面积对土冻结特征曲线影响的试验研究
1
2021
... 受孔隙几何效应和土颗粒表面作用的影响,冻土内部始终存在一定数量的未冻水,未冻水即使在极低的温度下也依然存在.按照成因,冻土中的未冻水可分为两种类型:薄膜未冻水和毛细未冻水[29].如图1所示,薄膜未冻水因预熔作用形成,赋存在土颗粒表面,受土颗粒强烈的束缚作用.毛细未冻水因孔隙力学作用产生,赋存在孔隙之中.在黏土、粉质黏土和粉土等塑性较强的细粒土中,未冻水含量较为显著[30]. ...
Modelling of cryogenic processes in permafrost and seasonally frozen soils
1
2009
... 根据热力学Clapeyron方程,低温吸力sc可近似用下式计算[31]. ...
Some aspects of effective stress in saturated and partly saturated soils
1
1963
... 由于冻土内部冰-水-土相互作用的复杂性,目前冻土的有效应力理论尚不成熟,各研究中存在不同的有效应力表示方法.目前常用的有效应力表达方法有Bishop应力法[32]、净应力法[23]和固相应力法[33].Bishop应力法借鉴了非饱和土中Bishop应力的定义方式,采用下式计算冻土中的有效应力. ...
Constitutive model for long-term behavior of saturated frozen soil
1
2017
... 由于冻土内部冰-水-土相互作用的复杂性,目前冻土的有效应力理论尚不成熟,各研究中存在不同的有效应力表示方法.目前常用的有效应力表达方法有Bishop应力法[32]、净应力法[23]和固相应力法[33].Bishop应力法借鉴了非饱和土中Bishop应力的定义方式,采用下式计算冻土中的有效应力. ...
Modeling the combined effect of time and temperature on normally consolidated and overconsolidated clays
1
2020
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
An advanced UH model for unsaturated soils
0
2020
Time-dependent unified hardening model: three-dimensional elastoviscoplastic constitutive model for clays
1
2015
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
Experimental study of a pseudo-preconsolidation pressure in frozen soils
1
2010
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
Experimental research on preconsolidation pressure of frozen soil
1
2009
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
冻土前期固结压力的试验研究
1
2009
... 土是一种多孔介质,其力学性质与孔隙含量(即密实度)有很大关系,而土的密实度又与土质类型、应力历史和含水率等诸多因素有关.在经典土力学中,超固结这一概念用来反映应力历史对黏性土密实度和刚度、强度等力学性质的影响.根据应力加载条件,室内土工试验中常见的土超固结特性可分为一维超固结性和三轴超固结性两种类型.一维超固结性主要体现为土的一维压缩曲线具有前期固结压力这一特征,三轴超固结性主要体现为土的三轴剪切应力-应变曲线具有应变软化和剪胀特征.早期的土力学研究普遍仅考虑应力历史对土超固结性的影响,但后续更深入的研究发现温度、饱和度、蠕变等因素也会引起土密实度和力学参数的变化,从而影响土的前期固结压力、应变软化和剪胀等超固结性[34-36].关于冻土,Qi等[37]、胡伟等[38]通过饱和冻结青藏粉质黏土的侧限压缩试验发现冻土具有与融土超固结性类似的表观超固结性,Nishimura等[22-23]指出低温吸力引起冻土表观超固结度的改变.由此可见,可以将超固结的概念引入冻土力学从而分析冻土的力学特性.本研究通过室内侧限压缩试验和三轴剪切试验研究低温粒间吸力对冻土表观超固结性的影响.由于以目前的试验手段难以控制和测量低温吸力,又考虑到低温粒间吸力和温度间具有一一对应关系[式(2)],本研究通过控制土样温度的方法来改变低温粒间吸力的大小. ...
Development and application of a confined compression apparatus for frozen soil
1
2019
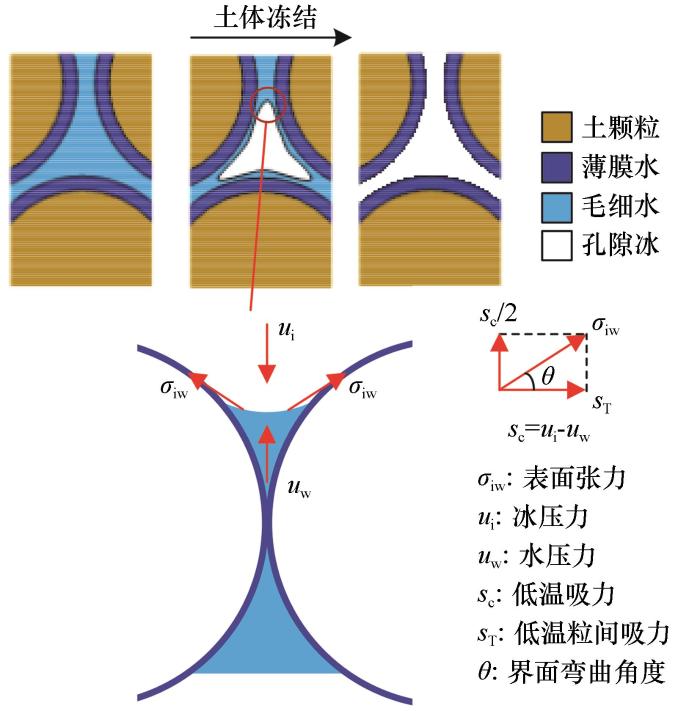
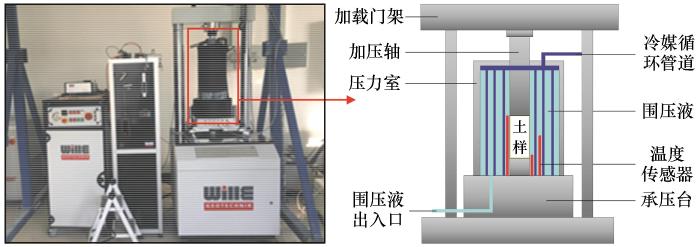
... 侧限压缩试验依托自主研发的DCYY-100型冻土侧限压缩仪进行[39],仪器照片和组成示意图见图3.试样为直径61.8 mm、高150 mm的圆柱体,放置在由304不锈钢制作的压力室内.压力室侧壁刚度极大,可有效限制土样侧向变形.压力室侧壁分为内外两层,两层之间贴有水平应变片.根据应变片监测到的侧壁微弱变形,可计算土样受到的侧向压力.土样受到的轴向力由高性能负荷门式框架施加,轴向力最大值为100 kN,力值误差±1%.土样控温采用恒温箱和循环冷浴相结合的二级控温方法.首先,压力室放置在冷却罐中,冷却罐内装有高标号液压油.通过冷浴对液压油进行低温控制,实现对土样的一级控温.其次,冷却罐整体放在恒温箱之中,通过恒温箱控制冷却罐周围环境温度,实现对土样的二级控温.通过以上二级控温措施,该仪器可在-30~60 ℃范围内实现对土样温度的精确控制,控温精度达±0.1 ℃.土样的底部插有温度探头,可实时监测土样温度. ...
冻土侧限压缩试验仪的研制及应用
1
2019
... 侧限压缩试验依托自主研发的DCYY-100型冻土侧限压缩仪进行[39],仪器照片和组成示意图见图3.试样为直径61.8 mm、高150 mm的圆柱体,放置在由304不锈钢制作的压力室内.压力室侧壁刚度极大,可有效限制土样侧向变形.压力室侧壁分为内外两层,两层之间贴有水平应变片.根据应变片监测到的侧壁微弱变形,可计算土样受到的侧向压力.土样受到的轴向力由高性能负荷门式框架施加,轴向力最大值为100 kN,力值误差±1%.土样控温采用恒温箱和循环冷浴相结合的二级控温方法.首先,压力室放置在冷却罐中,冷却罐内装有高标号液压油.通过冷浴对液压油进行低温控制,实现对土样的一级控温.其次,冷却罐整体放在恒温箱之中,通过恒温箱控制冷却罐周围环境温度,实现对土样的二级控温.通过以上二级控温措施,该仪器可在-30~60 ℃范围内实现对土样温度的精确控制,控温精度达±0.1 ℃.土样的底部插有温度探头,可实时监测土样温度. ...
A new criterion for strength of frozen sand under quick triaxial compression considering effect of confining pressure
1
2007
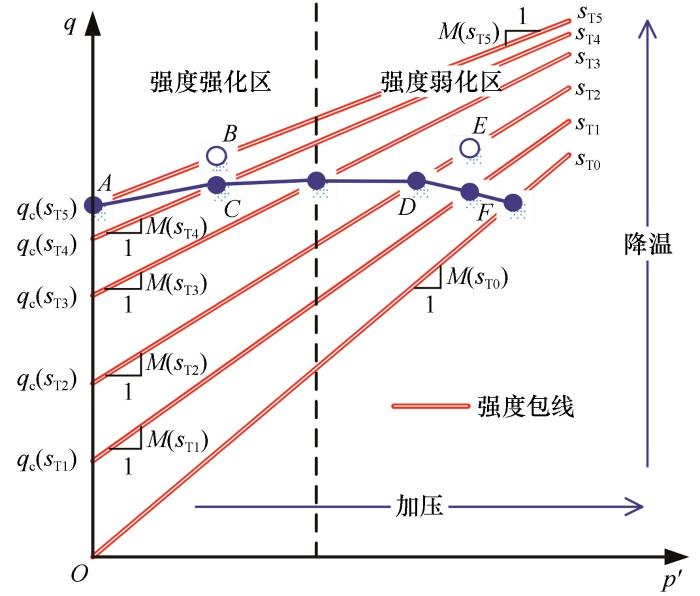
... 已有的大量试验研究表明冻土抗剪强度受温度和围压两个因素的显著影响,冻土抗剪强度随温度降低而增大,随围压增大而呈先增后减的趋势[40].在不考虑冰本身力学特性变化的前提下,温度和围压影响冻土强度的根源在于两者改变了冻土中的未冻水含量.考虑到前文所述低温粒间吸力和未冻水含量间具有一一对应的关系,则温度和围压对冻土强度的影响可用低温吸力理论解释. ...
Advanced UH models for soils
2
2015
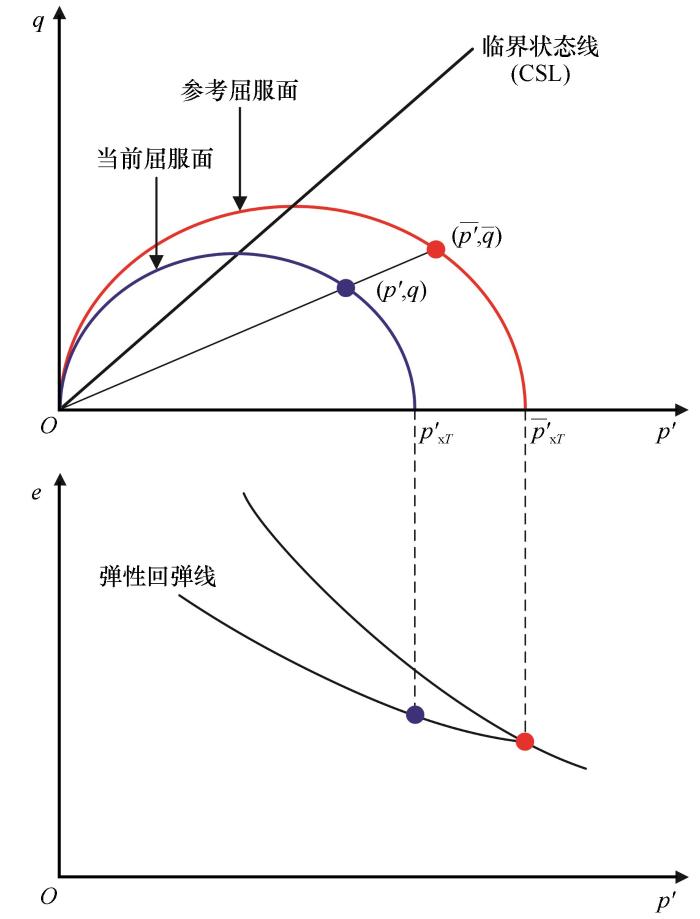
... 为了合理描述冻土在低温粒间吸力作用下产生的表观超固结特性和应力-应变关系,在姚仰平[41]提出的超固结土统一硬化本构模型(UH模型)基础上,通过采用冻土有效应力作为应力变量,构建了包含低温粒间吸力的屈服函数和硬化定律,进而建立了饱和冻土的弹塑性本构模型. ...
... 当前屈服面对应土的超固结状态.超固结土在加载过程中会先剪缩、后剪胀,因此在整个加载过程中不是单调变化的,不能被用来描述超固结土的硬化.本文采用姚仰平[41]提出的统一硬化参数H作为当前屈服面的硬化参数,则当前屈服面的硬化定律为 ...
UH模型系列研究
2
2015
... 为了合理描述冻土在低温粒间吸力作用下产生的表观超固结特性和应力-应变关系,在姚仰平[41]提出的超固结土统一硬化本构模型(UH模型)基础上,通过采用冻土有效应力作为应力变量,构建了包含低温粒间吸力的屈服函数和硬化定律,进而建立了饱和冻土的弹塑性本构模型. ...
... 当前屈服面对应土的超固结状态.超固结土在加载过程中会先剪缩、后剪胀,因此在整个加载过程中不是单调变化的,不能被用来描述超固结土的硬化.本文采用姚仰平[41]提出的统一硬化参数H作为当前屈服面的硬化参数,则当前屈服面的硬化定律为 ...
Experimental study on strength properties of artificial frozen soil in marine soft soil area of Ningbo City, China
1
2017
... 使用所提模型对文献中多种类型冻土的单轴压缩试验结果进行预测,包括宁波粉质黏土、粉土和淤泥质土[42]以及祁南黏土[43]、和林黄土[17],预测应力-应变曲线如图15所示.图中ε1为轴向应变,预测所用参数见表1.从图中可以看出,本文模型能够反映冻土单轴抗压强度随温度降低而升高的试验规律.并且,对于宁波粉质黏土、祁南黏土、和林黄土,其应力-应变曲线的应变软化程度随温度降低而增强,本文模型能够描述这一规律. ...
宁波海相软弱土层人工冻土强度特性试验
1
2017
... 使用所提模型对文献中多种类型冻土的单轴压缩试验结果进行预测,包括宁波粉质黏土、粉土和淤泥质土[42]以及祁南黏土[43]、和林黄土[17],预测应力-应变曲线如图15所示.图中ε1为轴向应变,预测所用参数见表1.从图中可以看出,本文模型能够反映冻土单轴抗压强度随温度降低而升高的试验规律.并且,对于宁波粉质黏土、祁南黏土、和林黄土,其应力-应变曲线的应变软化程度随温度降低而增强,本文模型能够描述这一规律. ...
Experimental study on uniaxial unconfined compressive strength of artificial frozen clay
1
2020
... 使用所提模型对文献中多种类型冻土的单轴压缩试验结果进行预测,包括宁波粉质黏土、粉土和淤泥质土[42]以及祁南黏土[43]、和林黄土[17],预测应力-应变曲线如图15所示.图中ε1为轴向应变,预测所用参数见表1.从图中可以看出,本文模型能够反映冻土单轴抗压强度随温度降低而升高的试验规律.并且,对于宁波粉质黏土、祁南黏土、和林黄土,其应力-应变曲线的应变软化程度随温度降低而增强,本文模型能够描述这一规律. ...
人工冻黏土单轴无侧限抗压强度试验研究
1
2020
... 使用所提模型对文献中多种类型冻土的单轴压缩试验结果进行预测,包括宁波粉质黏土、粉土和淤泥质土[42]以及祁南黏土[43]、和林黄土[17],预测应力-应变曲线如图15所示.图中ε1为轴向应变,预测所用参数见表1.从图中可以看出,本文模型能够反映冻土单轴抗压强度随温度降低而升高的试验规律.并且,对于宁波粉质黏土、祁南黏土、和林黄土,其应力-应变曲线的应变软化程度随温度降低而增强,本文模型能够描述这一规律. ...
Experimental test on constitutive relationship of Nanjing frozen silty clay considering Duncan-Chang model
1
2014
... Lai等[15]对青藏粉土、Xu等[21]对砂土、孙谷雨等[44]对南京粉质黏土在不同温度下进行了三轴剪切试验.使用表1参数对以上试验进行预测,试验数据与计算结果对比见图16.由于以上文献中没有提供体应变数据,因此仅给出了体应变的预测结果.图16(a)中,随着温度的降低,冻结砂土的应力-应变曲线由应变硬化型逐渐过渡为应变软化型,体应变曲线逐步由剪缩型过渡为剪胀型,这都表明冻土的表观超固结度随温度降低而增强.图16(b)中,冻结粉土的应力-应变曲线均为应变软化型,体应变曲线均为剪胀型,但应变软化程度和剪胀程度随着温度的降低而增强,也即表观超固结度随温度降低而增强.图16(c)中,应力-应变曲线均为应变硬化型,体应变曲线均为剪缩型,但随着温度降低,应力-应变曲线的峰值强度升高,体应变曲线的剪缩量减小.由以上各图可知,本文模型能够较好地反映温度对冻土应变软化程度和剪胀性的影响,也能较好描述冻土抗剪强度(包括峰值强度和残余强度)随温度降低而增大的规律. ...
南京地区冻结粉质黏土邓肯-张模型参数试验研究
1
2014
... Lai等[15]对青藏粉土、Xu等[21]对砂土、孙谷雨等[44]对南京粉质黏土在不同温度下进行了三轴剪切试验.使用表1参数对以上试验进行预测,试验数据与计算结果对比见图16.由于以上文献中没有提供体应变数据,因此仅给出了体应变的预测结果.图16(a)中,随着温度的降低,冻结砂土的应力-应变曲线由应变硬化型逐渐过渡为应变软化型,体应变曲线逐步由剪缩型过渡为剪胀型,这都表明冻土的表观超固结度随温度降低而增强.图16(b)中,冻结粉土的应力-应变曲线均为应变软化型,体应变曲线均为剪胀型,但应变软化程度和剪胀程度随着温度的降低而增强,也即表观超固结度随温度降低而增强.图16(c)中,应力-应变曲线均为应变硬化型,体应变曲线均为剪缩型,但随着温度降低,应力-应变曲线的峰值强度升高,体应变曲线的剪缩量减小.由以上各图可知,本文模型能够较好地反映温度对冻土应变软化程度和剪胀性的影响,也能较好描述冻土抗剪强度(包括峰值强度和残余强度)随温度降低而增大的规律. ...


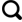





 甘公网安备 62010202000676号
甘公网安备 62010202000676号