0 引言
青藏高原分布着我国70%以上的多年冻土,是世界上中低纬度海拔最高、冻土分布最广的区域[1-2]。高原冻土区广泛分布的各类大型工程构筑物强烈影响土壤的传热,最终改变多年冻土的热平衡和温度场[3-5],导致多年冻土出现了明显的退化,给区域内各项重大线性工程的修建与运营带来了新的问题与挑战[6-8]。就实际工程而言,靠近起始冻结温度的负温区域(近相变区)冻土导热系数恰是影响工程热稳定性的关键物性参数。而实现对近相变区冻土导热系数的测量需要极高的控温和热流监测精度,限于成本及实验难度,目前尚未形成相对成熟的近相变区冻土导热系数测试方法。因此,如何精确地测定近相变区冻土导热系数对于描述冻土工程温度场分布、确保工程安全有着至关重要的作用。
经过多年发展,关于冻融土体导热系数的研究已在各方面取得诸多进展。国内外学者采用不同试验方法对冻融土导热系数开展了大量研究工作。例如,徐学祖等[9]利用量热法、热流计法和探针法等方法测量了不同冻土的导热系数,并编制了国内最早的冻土热参数表。Lu等[10]、Li等[11]、Zhang等[12]使用瞬态热线法对风积砂土、黏土和粉质黏土的导热系数进行了一系列测试研究。随着理论与技术的发展,也有不少学者对导热系数测试系统和测试方法进行了改进研发。例如,Alrtimi等[13]在稳态对比法冻土导热系数试验装置中增加了热套组件,可以极大程度减少测试装置的径向热损失,提高测试准确性;Kojima等[14]设计了一种新型双探头热脉冲传感器测量冻土热物性。
由于冻土导热系数试验测量成本高、耗时长且通常样本量有限,为更便于工程应用,研究人员以冻土导热系数实测数据为基础,通过线性回归、归一化等方法总结了大量的冻土导热系数计算模型。如,Lu等[15]对12种天然土壤进行了一系列热TDR测试,并提出了一种适用于广泛土壤水分条件的线性预测模型。Yan等[16]为测得从干燥到饱和的各种质地土壤的导热系数,开发了广义有效土壤导热系数模型。一些学者[17-18]对该模型进行了改进,以获得更广泛的适用性和更高的预测精度。如,Bi等[19]综合考虑土体组成和冻胀,提出冻土导热系数的广义计算模型。Lu等[20]综合考虑了温度、体积未冻水含量、孔隙率等因素建立冻结过程中热-水-变形相互作用的土壤导热系数模型,该模型能很好地反映冻结过程中水冰相变对土壤导热系数的影响。近年来,随着机器学习的成熟及其在处理复杂非线性问题方面的优势,许多研究人员已将其应用于土壤导热系数的预测[21-22]。例如,Bang等[23]研究了线性回归和各种机器学习方法在预测压实膨润土导热系数中的应用效果,并验证了机器学习方法预测土壤导热系数的可行性和优越性。
此外,近年来也有学者对近相变区冻土导热系数测试方法与预测模型开展了探索研究。如,Zhao等[24]结合稳态法和瞬态法,提出了一种在接近0 ℃下测量冻土导热系数的测试方法;李顺群等[25]建立了饱和冻土的复合传热模型及冻土导热系数模型,可计算得到0 ℃以下(-20~0 ℃)冻土导热系数随温度和含水量变化的理论值。夏锦红等[26]建立了考虑固-液界面的导热系数计算模型,可以有效模拟不同负温条件下冻土的导热系数。靳贻杰等[27]研究了-20~0 ℃两种含盐粉质黏土导热系数,并给出了不同条件下冻结温度和导热系数的经验公式。He等[28]采用稳态法对冻融灰泥土导热系数进行测试,发现土壤的相变主要发生在-3~-2 ℃。Firat等[29-30]提出了基于土壤内部因素和外部因素的人工神经网络预测模型,可有效预测-7~4 ℃不同温度下砂土的导热系数。
但应看到的是,现有冻土导热系数测试数据多为低温工况,近相变点附近的测试数据仍较为缺乏,且近相变区冻土导热系数的预测模型精度也有待提高。鉴于此,本文以青藏工程走廊内代表性土壤类型——细砂土为研究对象,提出了一种稳态热流计法试验测得导热系数、量子粒子群寻优算法计算定性温度的近相变区冻土导热系数测试方法,基于未冻水含量测试结果将导热系数测试区间划分近相变区和稳定相变区,分析了负温区细砂土导热系数的分布特征和参数影响规律,最终建立了近相变区导热系数预测模型,以期为未来冻土地区工程的修建提供合理的热参数指标。
1 试验方法
1.1 试验方案及流程
本研究首先采用基于稳态热流计法的试验装置测试获得近相变区细砂土样的名义导热系数,其测试原理为控制试样上下端保持一定温差,通过长时间热平衡使得试样内部达到近似一维稳态导热状态。此时,试样导热系数可由下式计算得到。
式中:q为热流量;λt 为名义测试温度为t时的名义导热系数,t一般取上下板的平均温度;A为样品传热面积;∆t为上下板温差;d为样品厚度。试验装置为HFM446(德国耐驰)导热系数测定仪,测试系统由Peltier系统、冷板、热流传感器、水浴装置、吹扫装置、稳压装置和数据采集装置构成,如图1所示。
图1
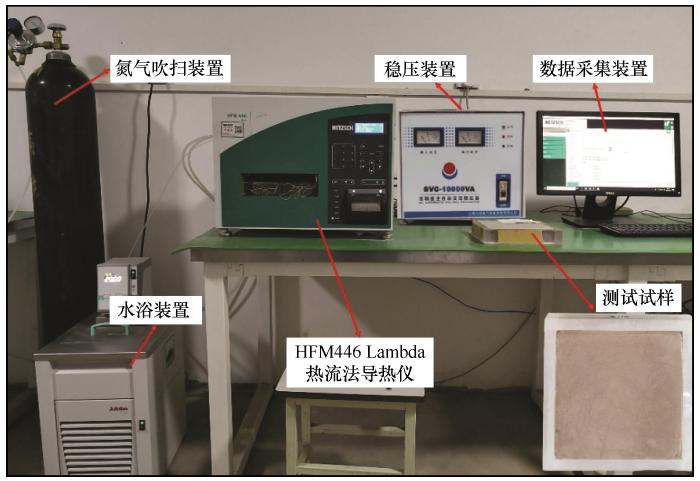
试验土样取自青藏公路典型路段清水河段(K2951),取样深度为0.5~2 m,试验用土为重塑土。将土样进行烘干、破碎、筛分后,取适量土样经过Bettersize2000激光粒度分布仪进行粒径分析,粒径分布如图2所示。测试试样的粒径分布范围为0.345~633.6 μm,粒径的主要分布区间(累计分布概率20%~80%)为92.01~267 μm。其中,黏粒 (<0.005 mm)、粉粒(0.005~0.075 mm)和砂粒 (>0.075 mm)的占比分别为5.13%、9.03%和85.84%。试样的体积加权平均径和比表面积分别为0.1975 mm和0.101 m2·g-1。根据《岩土工程勘察规范》(GB 50021—2001)[31]砂土分类标准,本文试验测试的土样为细砂土。
图2
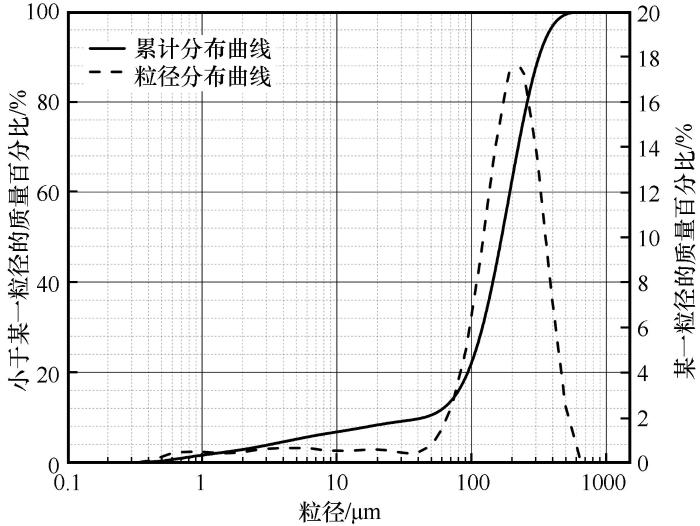
测试导热系数前需要对测试温度梯度下的校正因子N进行标定,标准试样材料为NIST1450D玻璃板,样品规格为200 mm×200 mm×25.5 mm,质量为2 214.08 g,密度为2.17 g·cm-3。测试导热系数将水浴设置为恒定温度12 ℃,打开氮气吹扫装置,先采用高流量吹扫气吹扫仪器内部的湿气,然后在测试过程中保持15 L·min-1的低流量持续吹扫,设置参数后开始测试,具体流程如图3所示。
图3
图3
细砂土导热系数测试流程
Fig. 3
Flow chart for testing thermal conductivity of fine sandy soil
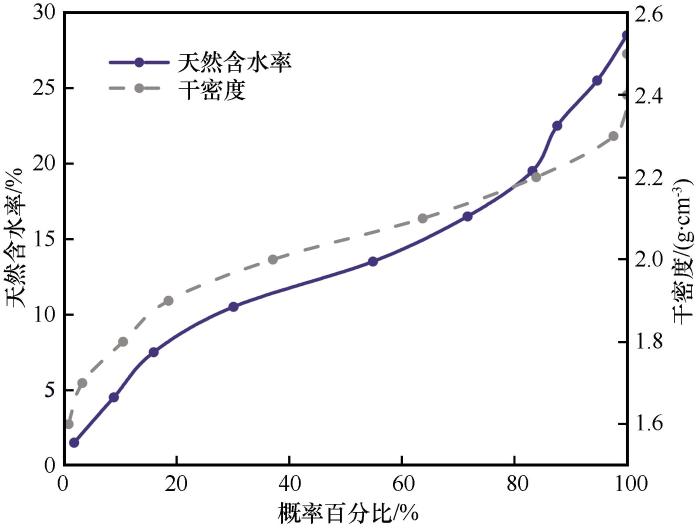
本课题组前期对青藏工程走廊沿线土样开展了大量土工测试工作[32-33],对其中124组细砂土样的天然含水率和干密度进行统计发现(结果如图4所示),天然含水率和干密度平均值分别为16.9%和2.03 g·cm-3,最小值和最大值分别为0.557%、29.8%和1.54 g·cm-3、2.39 g·cm-3。但考虑到细砂土黏性较低,且本研究试验土样规格为170 mm×170 mm×35.5 mm的扁平长方体,过大或过小干密度、含水率试样的制备存在一定难度,因此本文试验中试样的干密度控制范围为1.65~1.85 g·cm-3,以0.05 g·cm-3为干密度变化梯度;质量含水率控制范围为6%~14%,以2%为含水率变化梯度。同时,试验温度分为正温和负温两个区间:正温区间控制上下板温度为25/15 ℃;负温区间从试样相变点(冻结温度)附近开始向下降温,为了获得土体近相变区导热系数的变化情况,在-3.7~-0.5 ℃温度区间开展小温差间隔测试研究,详细试验方案见表1。
图4
图4
细砂土天然含水率和干密度累计概率分布
Fig. 4
Cumulative probability distribution of water content and dry density of fine sandy soil under natural conditions
表1 细砂土导热系数测试方案
Table 1
| 质量含水率/% | 干密度/(g·cm-3) | 上下冷板温度/℃ | 名义测试温度/℃ |
|---|---|---|---|
| 6 | 1.65,1.70,1.75,1.80,1.85 | 25/15,-0.5/-2.5,-0.7/-2.7,-0.9/-2.9,-1.2/-3.2,-1.7/-3.7,-2.7/-4.7,-4.7/-6.7,-7.7/-9.7,-11.7/-13.7 | 20,-1.5,-1.7,-1.9,-2.2,-2.7,-3.7,-5.7,-8.7,-12.7 |
| 8 | |||
| 10 | |||
| 12 | |||
| 14 |
1.2 导热系数定性温度近似回归
稳态法测试试样导热系数时,上下冷板始终存在着较大温度差,由于近相变区冻土导热系数的强烈非线性,若采用名义测试温度(上下冷板平均温度)作为测试导热系数对应的定性温度,则会存在较大误差。为此,本文通过量子粒子群寻优算法[34]近似回归得到名义导热系数对应的定性温度,具体步骤如下:
(1)假定冻土导热系数和定性温度的准确拟合公式为
(2)设定每一组测试的名义导热系数λd-i 对应的定性温度td-i,因每一组测试的名义导热系数λd-i 对应的定性温度td-i 在上下板温度区间的比例ki 是不一致的,因此设定试样在不同温度区间的导热系数对应的温度值td-i,如下式所示。
(3)通过Matlab软件进行程序编写,并将测试数据输入算法中,利用量子粒子群算法寻找上述公式内参数的最优值。将拟合得到的定性温度td-i 代入拟合函数中,求得该温度下的导热系数λd-i 与真实值λ*d-i 做出如下判断。
式中:ε、η为判定参数;n为测试温度点的个数;λd-i 为拟合导热系数;λ*d-i 为实测导热系数。当求得的λd-i 满足ε≤0.01时,拟合程序停止工作。ε≤η=0.01表示试样各温度点拟合得到的导热系数与测试的导热系数之间相对误差和小于0.01。
选取测试方案中含水率与干密度为中间值(w=10%,ρ=1.75 g·cm-3)的测试数据的拟合过程进行分析。不同相对误差和界限得到的导热系数与温度的拟合曲线如图5所示,图中平均值曲线是由各温度梯度的平均温度值与实测数据得出,10%、5%、1%表示ε≤0.10、ε≤0.05、ε≤0.01。由图可知,各曲线拟合得到的温度值分布于平均温度两侧,随着拟合精度的提高,高温区间的各拟合曲线的温度点逐渐减小,即向右偏移;低温区间的各拟合曲线温度点逐渐增大,即向左偏移。由此可见,样品两端的平均温度并非名义导热系数对应的定性温度,在近相变区定性温度低于样品两端的平均温度;在低温区定性温度高于样品两端的平均温度。以相对误差ε≤0.01为本文名义导热系数和定性温度拟合曲线。
图5
2 试验结果与分析
2.1 近相变温度区间划分
试样在冻结以后,毛细作用和土体颗粒表面的吸附作用使得土体内并非所有的液态水都被冻结,而这一部分未冻水与温度之间始终处于一种动态平衡的关系,其表达式[9]为
式中:wu为未冻水含量;θ为温度的绝对值;a、b为与土质相关的常数。表2为各试样未冻水含量与温度的拟合结果,以及各曲线斜率的平均值及其对应的温度值。
表2 各试样未冻水含量与温度的拟合关系
Table 2
| 试样编号 | ρd/(g·cm-3) | w/% | a | b | R2 | 曲线斜率的平均值 | 对应温度/℃ |
|---|---|---|---|---|---|---|---|
| 试样1 | 1.65 | 10 | 3.91 | -0.52 | 0.97 | -0.36 | -3.12 |
| 试样2 | 1.70 | 10 | 4.10 | -0.47 | 0.96 | -0.35 | -3.19 |
| 试样3 | 1.75 | 10 | 3.86 | -0.46 | 0.97 | -0.33 | -3.17 |
| 试样4 | 1.80 | 10 | 3.89 | -0.53 | 0.98 | -0.36 | -3.13 |
| 试样5 | 1.85 | 10 | 4.13 | -0.46 | 0.92 | -0.35 | -3.19 |
| 试样6 | 1.75 | 6 | 2.42 | -0.48 | 0.98 | -0.21 | -3.18 |
| 试样7 | 1.75 | 8 | 3.00 | -0.46 | 0.99 | -0.25 | -3.22 |
| 试样8 | 1.75 | 10 | 3.86 | -0.46 | 0.97 | -0.33 | -3.17 |
| 试样9 | 1.75 | 12 | 4.77 | -0.49 | 0.92 | -0.42 | -3.16 |
| 试样10 | 1.75 | 14 | 5.33 | -0.46 | 0.99 | -0.45 | -3.19 |
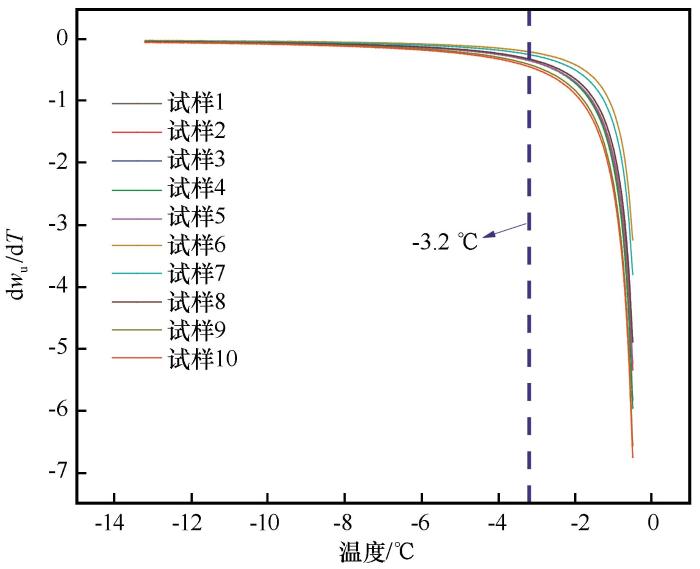
从表2可以看出,各试样未冻水含量与温度的R2均在0.9以上,未冻水变化速率平均值对应温度区间分布为-3.2~-3.1 ℃,其平均值为-3.17 ℃。图6为各试样的未冻水含量随温度变化速率,从图中可以看出,未冻水含量变化速率为单调函数,并且随着温度的升高,土样中未冻水随温度变化越来越快,温度低于-3.2 ℃时变化十分缓慢,越靠近0 ℃变化速率越快,近似呈指数增长。未冻水变化速率在一定程度上可以反映导热系数的变化,可以发现未冻水含量在-3.2~-0.5 ℃内变化十分剧烈,在-13.7~-3.2 ℃内变化相对缓慢,因此本文将-3.2~-0.5 ℃作为近相变区间,将-13.7~-3.2 ℃作为稳定相变区间。
图6
图6
未冻水含量随温度的变化速率
Fig. 6
Rate of change of unfrozen water content with temperature
2.2 近相变区细砂土导热系数参数影响规律
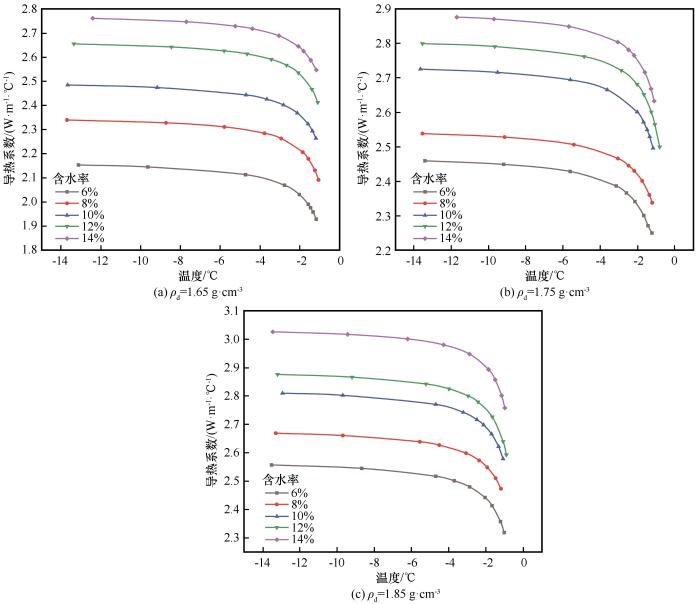
图7为不同干密度、含水率条件下细砂土试样导热系数随温度变化图。由图可知,土样导热系数的主要增幅区间为-3~-0.5 ℃,并且温度越靠近相变点,土样的导热系数的增幅也越大,增幅约占整个负温区导热系数总增幅的50%左右;当温度低于-3 ℃时,土样导热系数的增长幅度也逐渐趋于平缓,温度越低,导热系数的增长幅度越小。这是因为随着土样温度的降低,土样内的水分开始由液态转换为固态冰,并且冰的体积是水的1.1倍,冰的增加会使得土样内部的孔径被填充,从而增加了热流传递的接触面积,且固态冰也会令土体本身的导热性增强(冰的导热系数是水的4倍),因此土样的导热系数出现明显的增长幅度。另一方面近相变区土体内部冰水相变十分剧烈,稳态法测试热流沿垂直方向从上板流向下板,当样品内部达到热平衡需要更大的热流量q,在其他条件不变的情况下,热流量q增大,则会引起导热系数λ增大。当温度降低到-4 ℃左右,土体内的大部分水分已经冻结,因此图中导热系数随温度持续降低表现出增长缓慢的趋向。
图7
图7
不同干密度和含水率试样的导热系数随温度变化曲线
Fig. 7
Thermal conductivity curves of samples with different dry densities and water content with temperature
2.3 近相变区细砂土导热系数预测
2.3.1 拟合参数相关性分析
对细砂土过余温度、冻结导热系数和融土导热系数之间的偏相关性进行统计分析,结果如表3所示。由表可知,过余温度、融土导热系数和冻土导热系数之间呈显著相关关系。值得注意的是,在冻土导热系数与融土导热系数之间相关关系中,稳定相变区相关系数为0.843,近相变区为0.850,P值均小于0.01,说明冻土导热系数与融土导热系数之间有着极强的正相关关系。可以推断,融土导热系数结果隐含有决定土性成分和粒径等信息,可以利用融土导热系数用来预测冻土导热系数。
表3 细砂土近相变区导热系数与影响因素的偏相关分析
Table 3
| 区间 | 变量 | 参数 | 过余温度 | 融土导热系数 | 冻土导热系数 |
|---|---|---|---|---|---|
| 稳定相变区 | 过余温度 | 相关系数 | 1.000 | 0.269 | -0.318 |
| P值 | — | 0.002 | <0.001 | ||
| 融土导热系数 | 相关系数 | 0.269 | 1.000 | 0.843 | |
| P值 | 0.002 | — | <0.001 | ||
| 冻土导热系数 | 相关系数 | -0.318 | 0.843 | 1.000 | |
| P值 | <0.001 | <0.001 | — | ||
| 近相变区 | 过余温度 | 相关系数 | 1.000 | 0.249 | -0.292 |
| P值 | — | 0.013 | 0.004 | ||
| 融土导热系数 | 相关系数 | 0.249 | 1.000 | 0.850 | |
| P值 | 0.013 | — | <0.001 | ||
| 冻土导热系数 | 相关系数 | -0.292 | 0.850 | 1.000 | |
| P值 | 0.004 | <0.001 | — |
2.3.2 导热系数预测模型
对导热系数与过余温度、融土导热系数和冻土导热系数进行曲线估计后发现,在稳定相变区导热系数与三个因子之间呈线性关系,而在近相变区导热系数只与冻融土导热系数呈线性关系,与过余温度呈幂函数关系,故本文建立细砂土负温区导热系数分段预测模型为
式中:λ为导热系数(W·m-1·℃-1);Te为过余温度(℃);λu和λf分别为融土导热系数和冻土导热系数(W·m-1·℃-1);a、b、c、d均为待定拟合参数。拟合结果见表4。
表4 负温测试区间导热系数拟合的相关参数
Table 4
| 区间 | 拟合参数 | |||
|---|---|---|---|---|
| a | b | c | d | |
| 稳定相变区(-13.7~-3.2 ℃) | -0.590 | -0.040 | 0.729 | 0.605 |
| 近相变区(-3.2~-0.5 ℃) | -0.231 | 0.013 | 0.703 | 0.592 |
2.3.3 预测结果对比分析
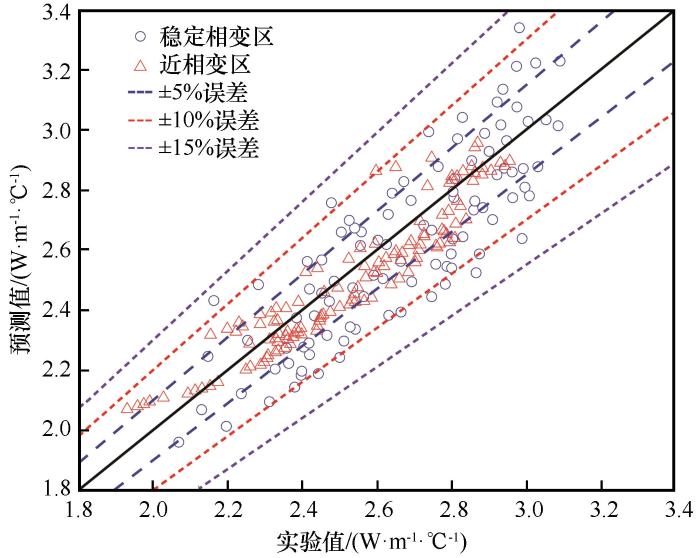
图8为细砂土近相变区导热系数预测结果与实验值对比,可见该预测模型预测值与实验值整体吻合良好,绝大多数样本预测点都分布在10%误差范围内,近相变区±10%误差范围内的预测结果占比99.3%,稳定相变区占比为88.9%,证明了该方法的有效性以及具备一定的工程应用价值。此外,稳定相变区的预测结果分布较为分散、范围更广,导热系数预测结果分布在2.01~3.34 W·m-1·℃-1之间,近相变区导热系数预测结果分布更为集中,导热系数预测结果分布在2.07~2.96 W·m-1·℃-1之间。
图8
图8
细砂土负温测试区间导热系数预测结果
Fig. 8
Prediction results of thermal conductivity of fine sandy soil in the negative temperature testing range
表5为近相变区导热系数预测模型的平均相对误差、最大误差估计和误差在±15%、±10%和±5%内的占比以及确定系数R2。从表中可以看出,稳定相变区和近相变区的平均相对误差以及最大误差分别为3.10%、10.19%和5.45%、12.39%,总体平均相对误差为4.14%。稳定相变区预测结果在±15%、±10%和±5%误差内占比分别为100%、88.9%和45.5%,近相变区为100%、99.3%和83.3%,整个模型占比为100%、94.7%和66.7%。稳定相变区和近相变区预测模型确定系数R2分别为0.892和0.883,说明本文所提出预测模型具有较高预测精度。
表5 负温测试区间导热系数预测模型的预测结果
Table 5
| 区间 | 平均相对误差 | 最大误差 | ±15%误差内占比 | ±10%误差内占比 | ±5%误差内占比 | R2 |
|---|---|---|---|---|---|---|
| 稳定相变区 | 3.10% | 10.19% | 100% | 88.9% | 45.5% | 0.892 |
| 近相变区 | 5.45% | 12.39% | 100% | 99.3% | 83.3% | 0.883 |
| 整个温度区间 | 4.13% | 12.39% | 100% | 94.7% | 66.7% | — |
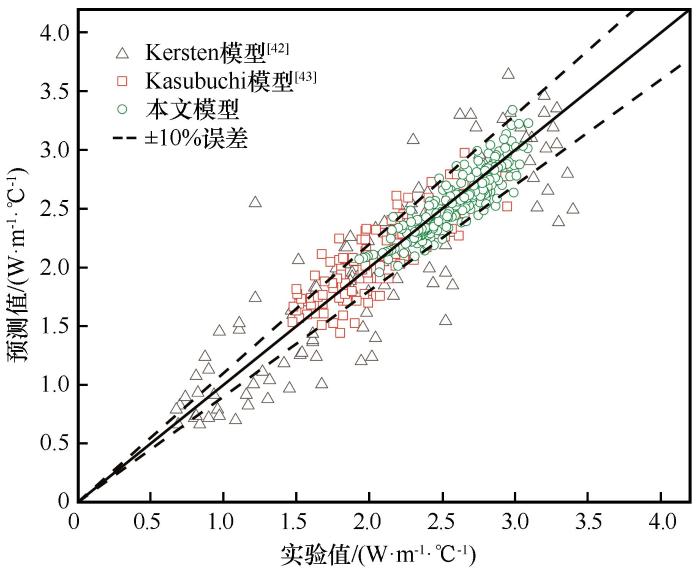
图9
图9
不同模型导热系数预测结果
Fig. 9
Prediction results of thermal conductivity of different models
3 结论
本文采用稳态热流计法获取近相变区细砂土导热系数,通过量子粒子群寻优算法确定名义导热系数对应的定性温度,并分析了导热系数的分布特征和参数影响规律。采用核磁共振技术对细砂土近相变区未冻水含量进行了测试并探究了其与导热系数的关系,基于未冻水含量测试结果将导热系数测试区间划分近相变区间和稳定相变区,建立细砂土近相变区导热系数预测模型,得出如下主要结论:
(1)负温区细砂土未冻水含量的变化曲线与其导热系数呈现出极为相似的变化规律,试样未冻水含量测试结果表明,负温区导热系数分析区间可划分为稳定相变区和近相变区,稳定相变区温度范围为-13.7~-3.2 ℃,近相变区温度范围为-3.2~-0.5 ℃。
(2)冻结细砂土导热系数的增幅区间主要发生在近相变区,增长幅度约占整个负温区导热系数总增幅的50%左右,且随温度降低,导热系数的增幅逐渐减小。
(3)通过拟合得到细砂土负温区导热系数预测模型,稳定相变区确定系数R2为0.892,近相变区确定系数R2为0.883。近相变区预测模型与测试值平均相对误差为5.45%,±15%误差内占比为100%,±10%误差内占比为99.3%,±5%误差内占比为83.3%,说明所提预测模型具有较高精度,可为近相变区细砂土导热系数的预测提供理论支撑。
参考文献
Impacts of climatic change on permafrost and cold regions environments in China
[J].
气候变化对中国多年冻土和寒区环境的影响
[J].
A new method to model the thermal conductivity of soil-rock media in cold regions: an example from permafrost regions tunnel
[J].
Lateral thermal disturbance of embankments in the permafrost regions of the Qinghai-Tibet engineering corridor
[J].
Experimental studies of thermal conductivity of undisturbed permafrost at Beiluhe testing site on the Tibetan Plateau
[J].
青藏高原北麓河地区原状多年冻土导热系数的试验研究
[J].
Distresses and countermeasures of highway subgrade in plateau permafrost regions
[J].
高原冻土区公路路基病害及工程对策
[J].
Qinghai-Tibet Highway engineering geology in permafrost regions: review and prospect
[J].
青藏公路多年冻土地区公路工程地质研究回顾与展望
[J].
Non-stationary random vibration analysis of railway embankments in permafrost regions under train loads using the explicit time-domain method
[J].
列车荷载下冻土路基非平稳随机振动分析的时域显式法
[J].
Experimental study on the thermal conductivity of aeolian sand from the Tibetan Plateau
[J].
Statistical characteristics of the thermal conductivity of frozen clay at different moisture contents
[J].
Variation of the thermal conductivity of a silty clay during a freezing-thawing process
[J].
An improved steady-state apparatus for measuring thermal conductivity of soils
[J].
Sensitivity analysis of temperature changes for determining thermal properties of partially frozen soil with a dual probe heat pulse sensor
[J].
An improved model for predicting soil thermal conductivity from water content at room temperature
[J].
A generalized model for estimating effective soil thermal conductivity based on the Kasubuchi algorithm
[J].
Soil thermal conductivity parameterization establishment and application in numerical model of central Tibetan Plateau
[J].
青藏高原中部土壤热传导率参数化方案的确立及在数值模式中的应用
[J].
Thermal conductivity of quartz sands by thermo-time domain reflectometry probe and model prediction
[J].
A generalized model for calculating the thermal conductivity of freezing soils based on soil components and frost heave
[J].
Modeling thermal conductivity of soils during a freezing process
[J].
Assessment of soil thermal conduction using artificial neural network models
[J].
A unified soil thermal conductivity model based on artificial neural network
[J].
Application of machine learning methods to predict a thermal conductivity model for compacted bentonite
[J].
Measurement of thermal conductivity for frozen soil at temperatures close to 0 ℃
[J].
Study of thermal conductivity model of frozen soil skeleton
[J].
冻土导热系数骨架模型研究
[J].
Theoretical model and experimental verification on thermal conductivity of frozen soil under different negative temperature conditions
[J].
不同负温条件下冻土导热系数的理论模型和试验验证
[J].
Experimental study on freezing temperature and thermal conductivity of salty frozen soil
[J/OL].
含盐冻土冻结温度及导热系数试验研究
[J/OL].
Characterization of thermal conductivity of seasonally frozen turfy soil from Northeastern China
[J].
Investigation of the thermal conductivity of soil subjected to freeze-thaw cycles using the artificial neural network model
[J].
Experimental study and modelling of the thermal conductivity of frozen sandy soil at different water contents
[J].
Experimental test and prediction model of soil thermal conductivity in permafrost regions
[J].
Study on characteristic and prediction model of permafrost thermal diffusivity of Qinghai-Tibet engineering corridor
[J].
青藏工程走廊冻融土热扩散系数特性与预测模型研究
[J].
A global search strategy of quantum-behaved particle swarm optimization
[C]// 2004 IEEE Conference on Cybernetics and Intelligent Systems: vol
A soil freezing characteristic curve model for capturing void ratio and specific surface area effects
[J].
考虑土体孔隙比和比表面积影响的未冻结体积含水率曲线模型
[J].
Study on the variation law of unfrozen water based on the new technology of layered nuclear magnetic testing: taking the freezing and thawing process of sand as an example
[J].
基于分层核磁测试新技术的未冻水变化规律研究: 以砂土冻融过程为例
[J].
Effects of compaction and water content on thermal conductivity of unsaturated soils
[J].
压实度和含水率对非饱和土导热系数的影响
[J].
Influence of porosity and water content on thermal properties of sandy soil sample
[J].
孔隙率与含水率对砂质土样导热系数的影响
[J].
Study on test and prediction method of thermal conductivity of dispersed clay
[J/OL].
分散性黏土导热系数试验与预测方法研究
[J/OL].
A numerical model for thermal conductivity of soft soils based on mesoscopic simulation
[J].
基于细观模拟的软土导热系数数值预测模型
[J].
Non-liner prediction of soil thermal conductivity based on RBF neural network
[J].
基于RBF神经网络的土体导热系数非线性预测
[J].
Laboratory research for the determination of the thermal properties of soils
[R].
Normalized thermal conductivity model for three Japanese soils
[J].


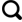




 甘公网安备 62010202000676号
甘公网安备 62010202000676号