Groundwater in the permafrost regions on the Qinghai-Tibet Plateau and it changes
1
2013
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
青藏高原多年冻土区地下水及其变化
1
2013
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
Change of temperature in Tibetan Plateau from 1961 to 2000
0
2001
Characteristics and differences of temperature rise between the Qinghai-Tibetan Plateau region and northwest arid region of China during 1960—2015
1
2019
... Comparison of the simulation accuracy of the two-input variable ELM model with the simulation results of other models
Table 7| 模型 | 平均NSE值 | 平均R值 | 研究区域 | 文献来源 |
|---|
| 20 cm | 40 cm | 65 cm | 20 cm | 40 cm | 65 cm |
|---|
| ELM | 0.91 | 0.84 | 0.83 | 0.96 | 0.94 | 0.91 | 风火山 | 本文 |
| BP | 0.76 | 0.65 | 0.69 | 0.89 | 0.84 | 0.84 | 风火山 | 本文 |
| SHAW | 0.87 | 0.85 | 0.91 | — | — | — | 风火山 | [19] |
| SHAW | 0.65 | 0.59 | 0.77 | 0.97 | 0.93 | 0.91 | 唐古拉山 | [3] |
| CoupModel | 0.84 | 0.91 | 0.81 | 0.96 | 0.97 | 0.93 | 风火山 | [14] |
| CoupModel | 0.88 | 0.84 | 0.67 | — | — | — | 风火山 | [18] |
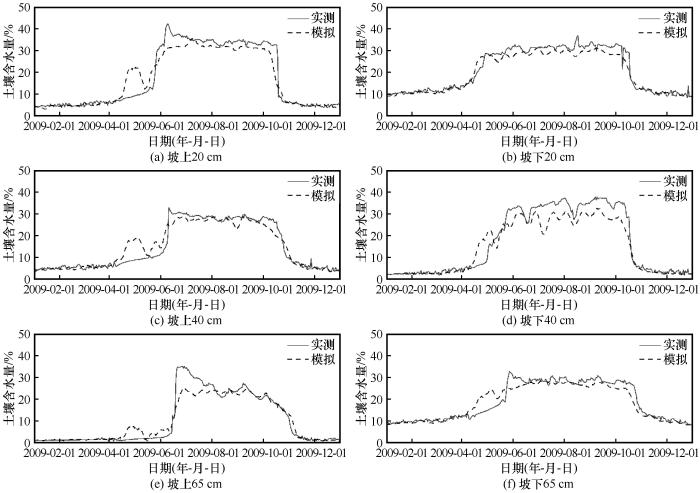
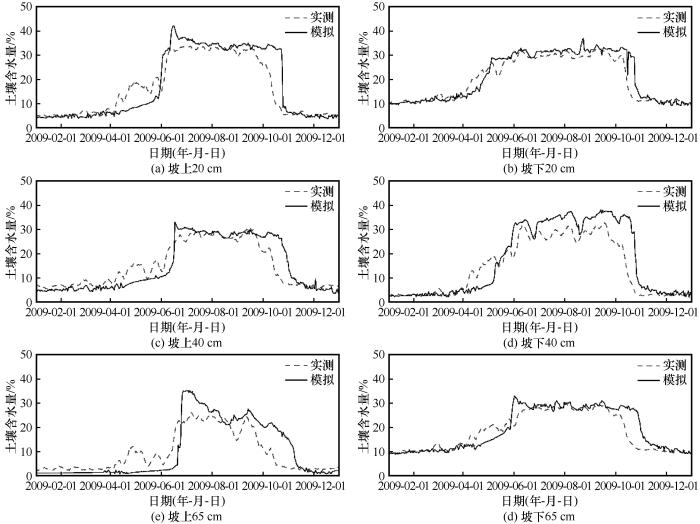
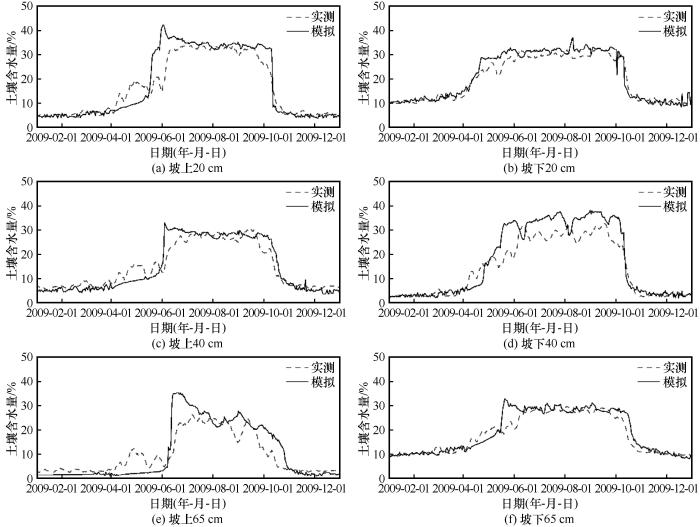
坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
1960—2015年青藏高寒区与西北干旱区升温特征及差异
1
2019
... Comparison of the simulation accuracy of the two-input variable ELM model with the simulation results of other models
Table 7| 模型 | 平均NSE值 | 平均R值 | 研究区域 | 文献来源 |
|---|
| 20 cm | 40 cm | 65 cm | 20 cm | 40 cm | 65 cm |
|---|
| ELM | 0.91 | 0.84 | 0.83 | 0.96 | 0.94 | 0.91 | 风火山 | 本文 |
| BP | 0.76 | 0.65 | 0.69 | 0.89 | 0.84 | 0.84 | 风火山 | 本文 |
| SHAW | 0.87 | 0.85 | 0.91 | — | — | — | 风火山 | [19] |
| SHAW | 0.65 | 0.59 | 0.77 | 0.97 | 0.93 | 0.91 | 唐古拉山 | [3] |
| CoupModel | 0.84 | 0.91 | 0.81 | 0.96 | 0.97 | 0.93 | 风火山 | [14] |
| CoupModel | 0.88 | 0.84 | 0.67 | — | — | — | 风火山 | [18] |
坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
Analysis of the climatic change characteristics in the southern Tibetan Plateau from 1971 to 2007
1
2010
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
1971—2007年青藏高原南部气候变化特征分析
1
2010
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
Analysis of soil moisture content in the active layer in the permafrost region of the Tuotuo River source in frozen season
4
2022
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
... 如图1所示,研究区域位于长江源区北麓河一级支流,左冒西孔曲小流域内(34°40′~34°48′ N,93°3′~92°50′ E),海拔分布在4 603~5 398 m[32].研究区域属于典型的连续多年冻土区,多年冻土层的厚度约为50~120 m,活动层厚度从0.8~2.5 m不等.全年平均气温为-5.2 ℃,年平均降水量在270 mm左右,年平均水面蒸发量高达1 480 mm左右.研究区域的山体坡度介于10°~15°之间,坡地植被类型以高寒草甸、高寒草原为主[33].受高寒草甸植被根系影响,0~30 cm土质较为疏松,含少量的风化砾石,土壤湿润.30 cm以下的土壤层含有较多的砾石,根系减少,土壤质地趋于紧密.活动层浅层土壤(0~50 cm)剖面植被根系分布较多,土壤有机质含量较高、黏性颗粒含量高、孔隙度大、容重较低.而深层土壤(50~100 cm)砂砾石含量逐渐增加,容重逐渐增加,有机质含量逐渐减少[5]. ...
... 坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
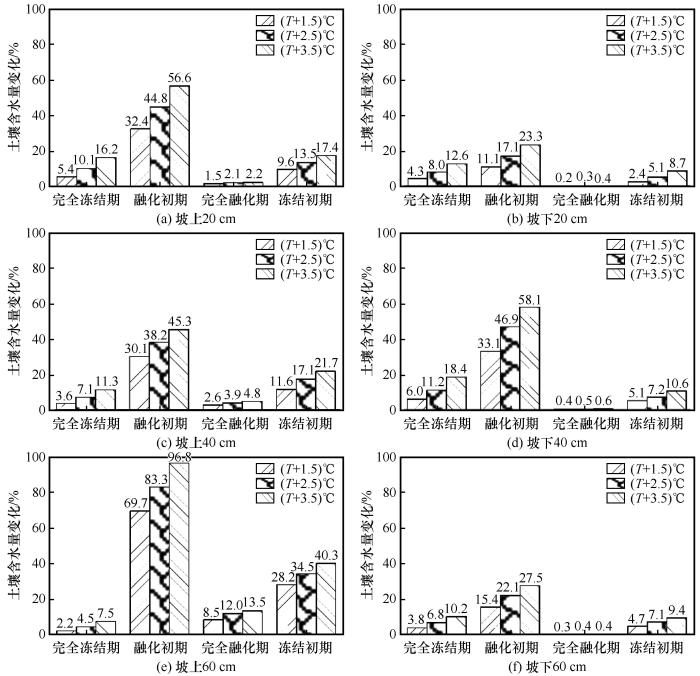
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
冻结季沱沱河源多年冻土区活动层土壤水分含量分析
4
2022
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
... 如图1所示,研究区域位于长江源区北麓河一级支流,左冒西孔曲小流域内(34°40′~34°48′ N,93°3′~92°50′ E),海拔分布在4 603~5 398 m[32].研究区域属于典型的连续多年冻土区,多年冻土层的厚度约为50~120 m,活动层厚度从0.8~2.5 m不等.全年平均气温为-5.2 ℃,年平均降水量在270 mm左右,年平均水面蒸发量高达1 480 mm左右.研究区域的山体坡度介于10°~15°之间,坡地植被类型以高寒草甸、高寒草原为主[33].受高寒草甸植被根系影响,0~30 cm土质较为疏松,含少量的风化砾石,土壤湿润.30 cm以下的土壤层含有较多的砾石,根系减少,土壤质地趋于紧密.活动层浅层土壤(0~50 cm)剖面植被根系分布较多,土壤有机质含量较高、黏性颗粒含量高、孔隙度大、容重较低.而深层土壤(50~100 cm)砂砾石含量逐渐增加,容重逐渐增加,有机质含量逐渐减少[5]. ...
... 坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
Impacts of changes in vegetation cover on soil water heat coupling in an alpine meadow of the Qinghai-Tibet Plateau, China
3
2009
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
... [6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
Permafrost degradation and ecological changes associated with a warming cliamte in central Alaska
1
2001
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
Boreal peatland C fluxes under varying permafrost regimes
2
2002
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
The impacts of climate extremes on the terrestrial carbon cycle: a review
1
2019
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
极端气候事件对陆地生态系统碳循环的影响
1
2019
... 近几十年来,全球变暖极大地改变了区域水文地质状况以及地下水动态,同时也影响了流域范围内水文过程及水资源的分布格局[1-4].土壤含水量在水、能量和碳循环等过程中具有重要意义,尤其在多年冻土区,土壤含水量是影响植被生长、地下水补给、地表径流、蒸散发以及冻融循环过程的重要因素[5],另一方面,冻融循环通过影响水文过程土壤水分的相变使土壤含水量发生变化[6].但是目前关于气候变化对土壤含水量的影响存在争议,气候变化可能导致冻土融化而引起浅层土壤含水量升高[7-8],也可能引起浅层土壤含水量减少,甚至区域蒸散发增加而出现干旱的情况[6].青藏高原作为“亚洲水塔”,广泛发育着多年冻土,为下游地区提供了大量水资源.准确评价未来气候变化对多年冻土区土壤含水量动态变化的影响具有重要意义[9]. ...
Coupled soil water and heat transfer modeling at local scale in the Yangtze River headwater region
1
2015
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
长江源区基于坡面尺度的土壤水热过程模拟研究
1
2015
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
Simulating the water-heat processes in permafrost regions in the Tibetan Plateau based on CoupModel
1
2012
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
基于CoupModel的青藏高原多年冻土区土壤水热过程模拟
1
2012
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
Energy-water balance of meadow ecosystem in cold frozen soil areas
3
2008
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
高寒冻土地区草甸草地生态系统的能量-水分平衡分析
3
2008
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
Seasonal dynamics of suprapermafrost groundwater and its response to the freeing-thawing processes of soil in the permafrost region of Qinghai-Tibet Plateau
4
2015
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
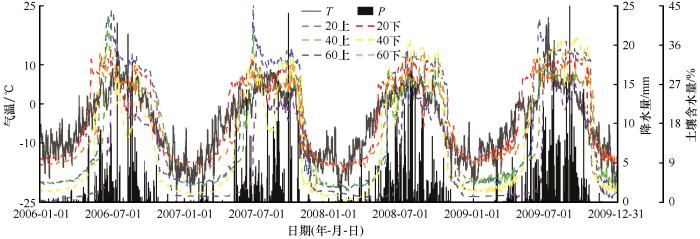
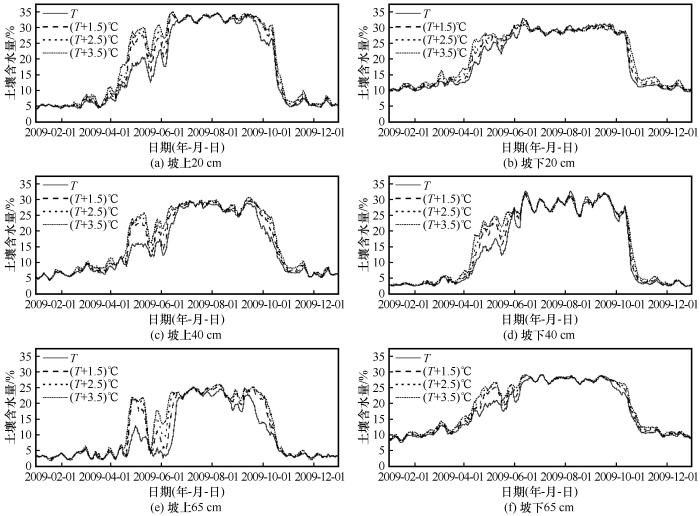
... 输入变量的选取对于人工智能模型的建立十分重要[13].输入变量一般选取与土壤含水量变化相关的影响因子.风火山流域相关研究表明[13,35],由于特殊的地理特征,对土壤含水量的影响因素较为复杂,但影响最大的因素主要是气温和降水.对2006—2009年数据统计分析也可以发现,融化期内,气温和降水与土壤含水量的变化趋势几乎一致(如图4所示),降水与土壤含水量之间有明显的相关性.同时过多的输入变量反而会使模型出现过拟合状态而降低模型的精度[13,20,35],所以将气温和降水作为预测土壤含水量的输入变量. ...
... [13,35],由于特殊的地理特征,对土壤含水量的影响因素较为复杂,但影响最大的因素主要是气温和降水.对2006—2009年数据统计分析也可以发现,融化期内,气温和降水与土壤含水量的变化趋势几乎一致(如图4所示),降水与土壤含水量之间有明显的相关性.同时过多的输入变量反而会使模型出现过拟合状态而降低模型的精度[13,20,35],所以将气温和降水作为预测土壤含水量的输入变量. ...
... [13,20,35],所以将气温和降水作为预测土壤含水量的输入变量. ...
Using neural networks for parameter estimation in ground water
2
2006
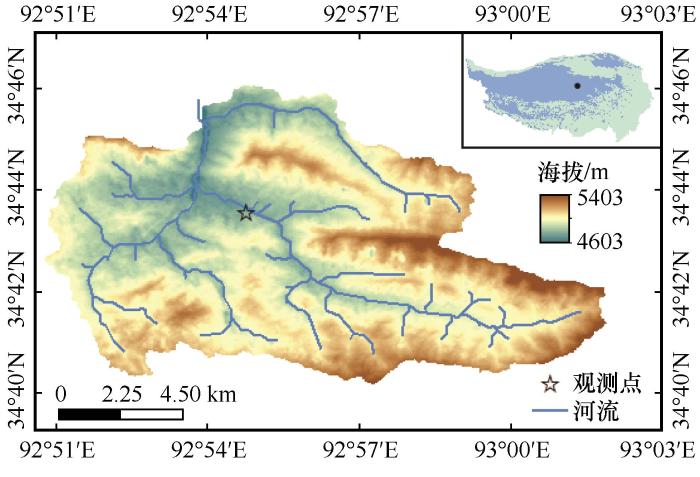
... ELM是一种基于单隐层前馈神经网络(SLFN)的学习算法模型,并已广泛应用于各种预测问题.ELM模型在训练过程中随机生成网络结构以及输入权值,通过训练得出输出权值,不需要调整其余任何参数,也就意味着ELM隐藏层节点的参数在隐藏层和训练数据之间是保持独立的[17-18].ELM避免了基于梯度递减的算法(如BP人工神经网络模型)学习速度慢,学习周期长,以及预测过程中出现局部最小值等问题.在ELM模型中,即使面对大数据和复杂的应用,输入数据的训练也是在秒和分钟的时间跨度完成的,这是传统技术无法实现的.在各种分类和回归的问题中,ELM模型相比于其他算法,其良好的泛化性能已经得到验证[14,23].图2是ELM的简化原理结构图. ...
... Comparison of the simulation accuracy of the two-input variable ELM model with the simulation results of other models
Table 7| 模型 | 平均NSE值 | 平均R值 | 研究区域 | 文献来源 |
|---|
| 20 cm | 40 cm | 65 cm | 20 cm | 40 cm | 65 cm |
|---|
| ELM | 0.91 | 0.84 | 0.83 | 0.96 | 0.94 | 0.91 | 风火山 | 本文 |
| BP | 0.76 | 0.65 | 0.69 | 0.89 | 0.84 | 0.84 | 风火山 | 本文 |
| SHAW | 0.87 | 0.85 | 0.91 | — | — | — | 风火山 | [19] |
| SHAW | 0.65 | 0.59 | 0.77 | 0.97 | 0.93 | 0.91 | 唐古拉山 | [3] |
| CoupModel | 0.84 | 0.91 | 0.81 | 0.96 | 0.97 | 0.93 | 风火山 | [14] |
| CoupModel | 0.88 | 0.84 | 0.67 | — | — | — | 风火山 | [18] |
坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
Streamflow forecasting using different artificial neural network algorithms
0
2007
Snow glacier melt estimation in tropical Andean glaciers using artificial neural networks
1
2013
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
Extreme learning machine: Theory and applications
2
2006
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... ELM是一种基于单隐层前馈神经网络(SLFN)的学习算法模型,并已广泛应用于各种预测问题.ELM模型在训练过程中随机生成网络结构以及输入权值,通过训练得出输出权值,不需要调整其余任何参数,也就意味着ELM隐藏层节点的参数在隐藏层和训练数据之间是保持独立的[17-18].ELM避免了基于梯度递减的算法(如BP人工神经网络模型)学习速度慢,学习周期长,以及预测过程中出现局部最小值等问题.在ELM模型中,即使面对大数据和复杂的应用,输入数据的训练也是在秒和分钟的时间跨度完成的,这是传统技术无法实现的.在各种分类和回归的问题中,ELM模型相比于其他算法,其良好的泛化性能已经得到验证[14,23].图2是ELM的简化原理结构图. ...
Extreme learning machine for regression and multiclass classification
3
2012
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... ELM是一种基于单隐层前馈神经网络(SLFN)的学习算法模型,并已广泛应用于各种预测问题.ELM模型在训练过程中随机生成网络结构以及输入权值,通过训练得出输出权值,不需要调整其余任何参数,也就意味着ELM隐藏层节点的参数在隐藏层和训练数据之间是保持独立的[17-18].ELM避免了基于梯度递减的算法(如BP人工神经网络模型)学习速度慢,学习周期长,以及预测过程中出现局部最小值等问题.在ELM模型中,即使面对大数据和复杂的应用,输入数据的训练也是在秒和分钟的时间跨度完成的,这是传统技术无法实现的.在各种分类和回归的问题中,ELM模型相比于其他算法,其良好的泛化性能已经得到验证[14,23].图2是ELM的简化原理结构图. ...
... Comparison of the simulation accuracy of the two-input variable ELM model with the simulation results of other models
Table 7| 模型 | 平均NSE值 | 平均R值 | 研究区域 | 文献来源 |
|---|
| 20 cm | 40 cm | 65 cm | 20 cm | 40 cm | 65 cm |
|---|
| ELM | 0.91 | 0.84 | 0.83 | 0.96 | 0.94 | 0.91 | 风火山 | 本文 |
| BP | 0.76 | 0.65 | 0.69 | 0.89 | 0.84 | 0.84 | 风火山 | 本文 |
| SHAW | 0.87 | 0.85 | 0.91 | — | — | — | 风火山 | [19] |
| SHAW | 0.65 | 0.59 | 0.77 | 0.97 | 0.93 | 0.91 | 唐古拉山 | [3] |
| CoupModel | 0.84 | 0.91 | 0.81 | 0.96 | 0.97 | 0.93 | 风火山 | [14] |
| CoupModel | 0.88 | 0.84 | 0.67 | — | — | — | 风火山 | [18] |
坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
Soil moisture forecasting by a hybrid machine learning technique: ELM integrated with ensemble empirical mode decomposition
2
2018
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... Comparison of the simulation accuracy of the two-input variable ELM model with the simulation results of other models
Table 7| 模型 | 平均NSE值 | 平均R值 | 研究区域 | 文献来源 |
|---|
| 20 cm | 40 cm | 65 cm | 20 cm | 40 cm | 65 cm |
|---|
| ELM | 0.91 | 0.84 | 0.83 | 0.96 | 0.94 | 0.91 | 风火山 | 本文 |
| BP | 0.76 | 0.65 | 0.69 | 0.89 | 0.84 | 0.84 | 风火山 | 本文 |
| SHAW | 0.87 | 0.85 | 0.91 | — | — | — | 风火山 | [19] |
| SHAW | 0.65 | 0.59 | 0.77 | 0.97 | 0.93 | 0.91 | 唐古拉山 | [3] |
| CoupModel | 0.84 | 0.91 | 0.81 | 0.96 | 0.97 | 0.93 | 风火山 | [14] |
| CoupModel | 0.88 | 0.84 | 0.67 | — | — | — | 风火山 | [18] |
坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
Daily streamflow prediction using optimally pruned extreme learning machine
1
2019
... 输入变量的选取对于人工智能模型的建立十分重要[13].输入变量一般选取与土壤含水量变化相关的影响因子.风火山流域相关研究表明[13,35],由于特殊的地理特征,对土壤含水量的影响因素较为复杂,但影响最大的因素主要是气温和降水.对2006—2009年数据统计分析也可以发现,融化期内,气温和降水与土壤含水量的变化趋势几乎一致(如图4所示),降水与土壤含水量之间有明显的相关性.同时过多的输入变量反而会使模型出现过拟合状态而降低模型的精度[13,20,35],所以将气温和降水作为预测土壤含水量的输入变量. ...
Monthly streamflow forecasting using ELM-IPSO based on phase space reconstruction
0
2020
Stream-flow forecasting using extreme learning machines: a case study in a semi-arid region in Iraq
2
2016
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... [22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
Prediction of soil moisture based on Extreme Learning Machine for an apple orchard
2
2015
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
... ELM是一种基于单隐层前馈神经网络(SLFN)的学习算法模型,并已广泛应用于各种预测问题.ELM模型在训练过程中随机生成网络结构以及输入权值,通过训练得出输出权值,不需要调整其余任何参数,也就意味着ELM隐藏层节点的参数在隐藏层和训练数据之间是保持独立的[17-18].ELM避免了基于梯度递减的算法(如BP人工神经网络模型)学习速度慢,学习周期长,以及预测过程中出现局部最小值等问题.在ELM模型中,即使面对大数据和复杂的应用,输入数据的训练也是在秒和分钟的时间跨度完成的,这是传统技术无法实现的.在各种分类和回归的问题中,ELM模型相比于其他算法,其良好的泛化性能已经得到验证[14,23].图2是ELM的简化原理结构图. ...
Forecasting daily runoff by extreme learning machine based on quantum-behaved particle swarm optimization
1
2017
... 一直以来,基于物理过程的数值模型被大量运用于多年冻土区土壤水热特征分析[10-12],由于在青藏高原等地区恶劣的气候环境,基础数据的获取往往具有较大的难度,因此机器学习工具成为一个较好的选择.近些年来,人工智能模型已经被广泛地运用到水文研究当中,甚至在多年冻土区的研究中也运用了人工智能模型模拟径流、地下水位、含冰量等[13-16].ELM(Extreme Learning Machine)是黄广斌等基于神经网络改进的智能模型,该模型使用前馈神经网络,具有较好的泛化能力[17-18].已有大量研究表明,ELM模型在对非冻土区地表径流、水分蒸发以及土壤含水量的模拟预测中达到较高的精度[19-22].Liu等[23]利用ELM和支持向量机(SVM)对澳大利亚维多利亚州Dookie苹果园的土壤含水量进行了预测,揭示了ELM在不同土壤深度的含水量预测的优越性能.Yaseen等[22]使用ELM对河流流量进行模拟预测发现,ELM模型在很多指标上优于支持向量回归(SVR)、广义回归神经网络(GRNN)以及其他模型.Niu等[24]通过将ELM模型和QPSO算法结合,对新丰江水库的逐日数据进行模拟,证实了ELM模型较好的泛化性.但是目前将ELM模型运用到对多年冻土区土壤含水量预测的研究很少,因此本研究希望通过运用ELM模型对多年冻土区土壤含水量的模拟进行尝试,为探究环境变化对多年冻土区水文过程的影响提供一种方法. ...
2
2021
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 由于各种因素对土壤含水量变化的影响具有一定的滞后性,以及研究区特殊的冻融变化过程,在模拟过程中发现,将模拟日期推迟一定的时间间隔时,模拟精度会有不同程度的提高或降低.本文两种模型的输出均用SM+1、SM+7、SM+14分别表示模型模拟的第1天、7天和14天的土壤含水量,以此分析当模型模拟时间向后延长时其模拟效果的变化.此外,在气候变化的背景下[25-26,28],设置了一定幅度气温升高、降水增加的情境,其中气温设置(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃三种变化,降水设置P+10%P、P+20%P、P+30%P三种变化,基于二输入变量模型一共进行9种交叉情境模拟,并且与原气温降水条件下的模拟结果进行对比. ...
The combined effects of warming and drying suppress CO2 and N2O emission rates in an alpine meadow of the eastern Tibetan Plateau
2
2012
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 由于各种因素对土壤含水量变化的影响具有一定的滞后性,以及研究区特殊的冻融变化过程,在模拟过程中发现,将模拟日期推迟一定的时间间隔时,模拟精度会有不同程度的提高或降低.本文两种模型的输出均用SM+1、SM+7、SM+14分别表示模型模拟的第1天、7天和14天的土壤含水量,以此分析当模型模拟时间向后延长时其模拟效果的变化.此外,在气候变化的背景下[25-26,28],设置了一定幅度气温升高、降水增加的情境,其中气温设置(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃三种变化,降水设置P+10%P、P+20%P、P+30%P三种变化,基于二输入变量模型一共进行9种交叉情境模拟,并且与原气温降水条件下的模拟结果进行对比. ...
Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model
1
2003
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
Broad range of 2050 warming from an observationally constrained large climate model ensemble
2
2012
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 由于各种因素对土壤含水量变化的影响具有一定的滞后性,以及研究区特殊的冻融变化过程,在模拟过程中发现,将模拟日期推迟一定的时间间隔时,模拟精度会有不同程度的提高或降低.本文两种模型的输出均用SM+1、SM+7、SM+14分别表示模型模拟的第1天、7天和14天的土壤含水量,以此分析当模型模拟时间向后延长时其模拟效果的变化.此外,在气候变化的背景下[25-26,28],设置了一定幅度气温升高、降水增加的情境,其中气温设置(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃三种变化,降水设置P+10%P、P+20%P、P+30%P三种变化,基于二输入变量模型一共进行9种交叉情境模拟,并且与原气温降水条件下的模拟结果进行对比. ...
Response of thermal-moisture condition within active layer in the hinterland of the Qinghai-Xizang Plateau to climate change
3
2021
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
青藏高原腹地多年冻土区活动层水热过程对气候变化的响应
3
2021
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
Changing tendency of precipitation in permafrost regions along Qinghai-Tibet Railway during last thirty years
1
2011
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
1976—2010年青藏铁路沿线多年冻土区降水变化特征
1
2011
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
Freezing and melting process of permafrost active layer near Wudaoliang in Qinghai-Tibet Plateau
1
2000
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
青藏高原五道梁附近多年冻土活动层冻结和融化过程
1
2000
... 研究表明,2011—2020年平均地表温度比1850—1900年高1.09 ℃(IPCC)[25],Shi等[26]、Sitch等[27]研究表明全球地表温度以0.3 ℃·(10a)-1上升,到本世纪末可能持续上升1.8~4.8 ℃.Rowlands等[28]通过模拟预测指出,预计到2050年全球气温将比上个世纪平均气温上升1.4~3.0 ℃.全球变暖已不可逆转,青藏高原对气温升高更为敏感,另有气象监测数据表明,风火山研究区域2001—2005年平均降雨量比1976—2010年多年平均降雨量增加近15%,2006—2010年平均降雨量更是高出20%以上[29-30].活动层土壤含水量的动态变化是影响寒区地下水循环和地表能量转换过程的主要因素[31].为了明晰气候变化下青藏高原多年冻土退化对区域水循环的影响,必须了解这些条件下活动层土壤水动态变化特征.因此,本研究基于获取的基础数据,根据青藏高原多年冻土冻融循环特征,将研究区域土壤含水量季节变化分为完全冻结期、融化初期、完全融化期和冻结初期四个时期[12],利用ELM模型对风火山研究区不同海拔、不同深度土壤含水量的动态变化过程进行模拟;并且在此基础上,设置了气温增加幅度分别为1.5 ℃、2.5 ℃、3.5 ℃[分别表示成(T+1.5) ℃、(T+2.5) ℃、(T+3.5) ℃]、降水量增加10%、20%、30%(分别表示成P+10%P、P+20%P、P+30%P)的气候变化情境,以分析不同海拔及不同深度土壤含水量对气候变化的响应特征. ...
Dynamic characteristics of condensed water in soils of Fenghuoshan Basin in Qinghai-Tibet Plateau
1
2012
... 如图1所示,研究区域位于长江源区北麓河一级支流,左冒西孔曲小流域内(34°40′~34°48′ N,93°3′~92°50′ E),海拔分布在4 603~5 398 m[32].研究区域属于典型的连续多年冻土区,多年冻土层的厚度约为50~120 m,活动层厚度从0.8~2.5 m不等.全年平均气温为-5.2 ℃,年平均降水量在270 mm左右,年平均水面蒸发量高达1 480 mm左右.研究区域的山体坡度介于10°~15°之间,坡地植被类型以高寒草甸、高寒草原为主[33].受高寒草甸植被根系影响,0~30 cm土质较为疏松,含少量的风化砾石,土壤湿润.30 cm以下的土壤层含有较多的砾石,根系减少,土壤质地趋于紧密.活动层浅层土壤(0~50 cm)剖面植被根系分布较多,土壤有机质含量较高、黏性颗粒含量高、孔隙度大、容重较低.而深层土壤(50~100 cm)砂砾石含量逐渐增加,容重逐渐增加,有机质含量逐渐减少[5]. ...
青藏高原风火山流域凝结水动态特征分析
1
2012
... 如图1所示,研究区域位于长江源区北麓河一级支流,左冒西孔曲小流域内(34°40′~34°48′ N,93°3′~92°50′ E),海拔分布在4 603~5 398 m[32].研究区域属于典型的连续多年冻土区,多年冻土层的厚度约为50~120 m,活动层厚度从0.8~2.5 m不等.全年平均气温为-5.2 ℃,年平均降水量在270 mm左右,年平均水面蒸发量高达1 480 mm左右.研究区域的山体坡度介于10°~15°之间,坡地植被类型以高寒草甸、高寒草原为主[33].受高寒草甸植被根系影响,0~30 cm土质较为疏松,含少量的风化砾石,土壤湿润.30 cm以下的土壤层含有较多的砾石,根系减少,土壤质地趋于紧密.活动层浅层土壤(0~50 cm)剖面植被根系分布较多,土壤有机质含量较高、黏性颗粒含量高、孔隙度大、容重较低.而深层土壤(50~100 cm)砂砾石含量逐渐增加,容重逐渐增加,有机质含量逐渐减少[5]. ...
Changes of grassland rain use efficiency and NDVI in northwestern China from 1982 to 2013 and its response to climate change
1
2018
... 如图1所示,研究区域位于长江源区北麓河一级支流,左冒西孔曲小流域内(34°40′~34°48′ N,93°3′~92°50′ E),海拔分布在4 603~5 398 m[32].研究区域属于典型的连续多年冻土区,多年冻土层的厚度约为50~120 m,活动层厚度从0.8~2.5 m不等.全年平均气温为-5.2 ℃,年平均降水量在270 mm左右,年平均水面蒸发量高达1 480 mm左右.研究区域的山体坡度介于10°~15°之间,坡地植被类型以高寒草甸、高寒草原为主[33].受高寒草甸植被根系影响,0~30 cm土质较为疏松,含少量的风化砾石,土壤湿润.30 cm以下的土壤层含有较多的砾石,根系减少,土壤质地趋于紧密.活动层浅层土壤(0~50 cm)剖面植被根系分布较多,土壤有机质含量较高、黏性颗粒含量高、孔隙度大、容重较低.而深层土壤(50~100 cm)砂砾石含量逐渐增加,容重逐渐增加,有机质含量逐渐减少[5]. ...
The response of soil moisture in swamp meadow in the source regions of the Yangtze River to artificially warming
3
2015
... 本研究所采用的数据资料来自于青藏高原风火山观测站.其中气温和降水数据由自动气象站观测所得,土壤含水量的观测分别由埋设在坡面两个位置(海拔分别为4 760 m、4 810 m)的20 cm、40 cm(浅层)以及65 cm(深层)[34]的频域反射仪(FDR)探头测量(观测精度为±2%),研究时段为2006—2009年.取所观测的土壤含水量、气温以及降水数据的日平均值作为当天数据. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
... [34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
长江源区沼泽草甸多年冻土活动层土壤水分对模拟增温的响应
3
2015
... 本研究所采用的数据资料来自于青藏高原风火山观测站.其中气温和降水数据由自动气象站观测所得,土壤含水量的观测分别由埋设在坡面两个位置(海拔分别为4 760 m、4 810 m)的20 cm、40 cm(浅层)以及65 cm(深层)[34]的频域反射仪(FDR)探头测量(观测精度为±2%),研究时段为2006—2009年.取所观测的土壤含水量、气温以及降水数据的日平均值作为当天数据. ...
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
... [34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
Simulation and prediction of suprapermafrost groundwater level variation in response to climate change using a neural network model
3
2015
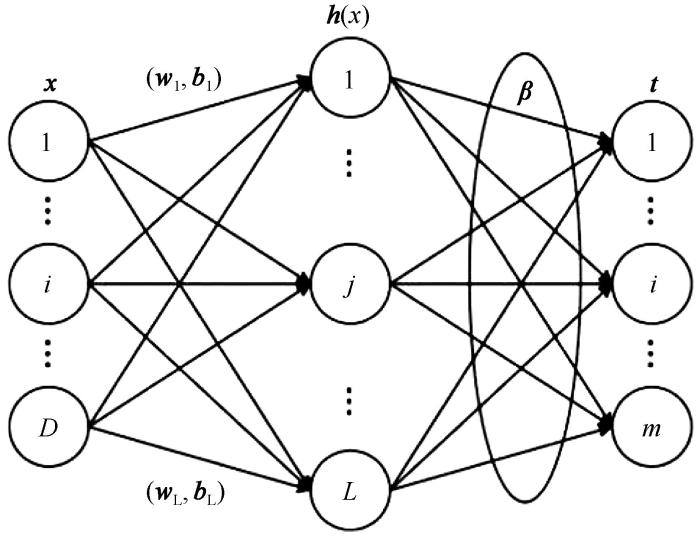
... 本文利用ELM模型,对研究区域2006—2009年土壤含水量的变化过程进行模拟.选择2006—2008年的数据作为训练序列,2009年数据作为验证序列.采用统计学中的偏自相关函数来确定模型输入变量的滞后天数,以此来确定各层深度土壤含水量的模拟时各影响因子的输入参数个数[35].该研究区域的土壤含水量偏自相关图如图3所示,滞后时间为5天时PACF图相关性较弱,考虑到研究区域数据匮乏以及收集数据难度大等情况,选择滞后天数为7天. ...
... 输入变量的选取对于人工智能模型的建立十分重要[13].输入变量一般选取与土壤含水量变化相关的影响因子.风火山流域相关研究表明[13,35],由于特殊的地理特征,对土壤含水量的影响因素较为复杂,但影响最大的因素主要是气温和降水.对2006—2009年数据统计分析也可以发现,融化期内,气温和降水与土壤含水量的变化趋势几乎一致(如图4所示),降水与土壤含水量之间有明显的相关性.同时过多的输入变量反而会使模型出现过拟合状态而降低模型的精度[13,20,35],所以将气温和降水作为预测土壤含水量的输入变量. ...
... ,35],所以将气温和降水作为预测土壤含水量的输入变量. ...
Analysis of thermal-moisture conditions of active layer and energy-water balance of land-atmosphere system in tanggula area
1
2020
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
唐古拉地区活动层水热状况及地气系统能水平衡分析
1
2020
... 张伟等[11]、徐洪亮等[29]分别运用CoupModel模型对风火山流域土壤含水量进行模拟发现,对活动层的冻融过程能较准确地模拟,但是对深层土壤含水量的模拟精度较低.郭林茂等[12]、周剑等[36]分别利用SHAW模型对青藏高原腹地土壤含水量进行模拟并指出气象、植被等参数的偏差会影响模型的模拟精度,而高寒地区各相关参数获取的难度会限制CoupModel以及SHAW等物理模型的模拟效果.本文二输入变量ELM模型对土壤含水量的模拟结果与其他模型模拟结果对比如表7所示.模拟结果显示,与原理相似的BP神经网络模型相比,二输入变量ELM模型对各深度土壤含水量的模拟效果均优于BP神经网络模型,可以得到更高的模拟精度.结果表明,若将更准确的影响参数和ELM模型结合,或可进一步提升模拟精度. ...
Soil moisture-heat migration characteristics within the permafrost active layer in Beiluhe
1
2015
... 坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
北麓河多年冻土活动层水热迁移规律分析
1
2015
... 坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
Weekly soil moisture forecasting with multivariate sequential, ensemble empirical mode decomposition and Boruta-random forest hybridizer algorithm approach
1
2019
... 坡下植被分布较坡上更加均匀,而且海拔相对较低,空气对流以及辐射的影响程度相对较小,气温、降水与土壤含水量变化之间的相关性更加稳定[5],导致坡下各深度土壤含水量模拟效果整体优于坡上.由于多年冻土区实际存在的未冻水在冻结锋面起到“热阻”的作用,对冻土的融化阶段和冻结阶段都会有一定的滞缓作用[37],所以模型对融化初期和冻结初期土壤含水量的模拟存在一定误差以及时间的滞后或提前.另外完全冻结时期与完全融化时期的模拟效果优于融化初期与冻结初期.Prasad等[38]运用混合ELM进行土壤含水量的模拟预测时发现,模型对夏季模拟效果较好,对春季和秋季的模拟误差较大,与本文模拟结果具有相似的规律. ...
Processes of soil thawing-freezing and features of soil moisture migration in the permafrost active layer
1
2014
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
多年冻土区活动层冻融状况及土壤水分运移特征
1
2014
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
Study on the influence of vegetation change on soil moisture cycle in alpine meadow
2
2003
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
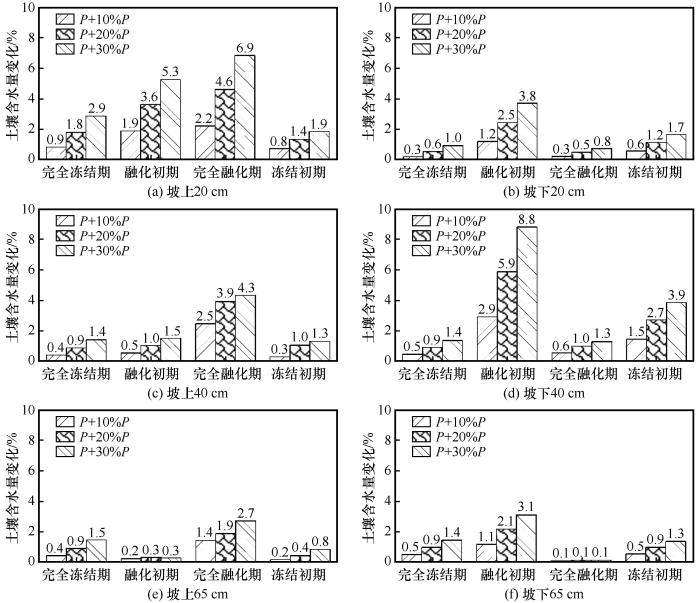
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
高寒草地植被覆盖变化对土壤水分循环影响研究
2
2003
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
Mechanism of climate warming on thermal-moisture dynamics of active permafrost layer considering effect of rainfall
2
2019
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
... [41]. ...
考虑降雨作用的气温升高对多年冻土活动层水热影响机制
2
2019
... 青藏高原对气候变化的响应具体表现为活动层厚度变大,温度升高,降水增加等趋势.在融化初期,随着气温的升高,表层土壤温度升高,上下层土壤之间的温差变大,此时温度梯度由浅层土壤指向深层土壤,加快活动层土壤融化过程;而活动层土壤在冻结初期需要向大气释放热量以降低土壤温度,在气温增加的情境下,表层土壤向大气释放热量降低温度的趋势减弱,从而滞缓了土壤水分冻结过程[39],在本文模拟过程中表现为融化初期土壤含水量因融化出现上升的时间提前,以及冻结初期土壤含水量因冻结出现下降的时间延迟的现象,且气温升幅越大,这种现象就越明显.徐洪亮等[29]利用CoupModel模型得到的结果与本文相似,并且指出土壤深度越大,融化时期持续时间的延长现象会更明显[6].在融化初期和冻结初期,土壤含水量对气温上升的响应较强烈,而且气温增幅越大,各层土壤含水量的增加趋势越显著.在融化初期,坡上65 cm深度土壤含水量增加率最大,坡下40 cm深度土壤含水量增加率最大;而在冻结初期,坡上、坡下均表现为深层土壤含水量增加较浅层更加明显.活动层土壤含水量的垂直剖面分布特征受植被类型、土壤质地以及水分迁移的影响,研究区内坡下植被发育相比于坡上更好,而坡上土壤含有较多的砾石,坡下土壤黏土比例较大,可能是造成坡上坡下垂向对升温的响应规律不同的原因[5,40].另外当升温幅度相同时,坡上各深度土壤含水量动态变化相比于坡下更具敏感性,说明可能在植被、土壤质地等差异下,气温变化对坡上土壤含水量变化影响更大.在完全冻结期间和完全融化期间,土壤含水量平均值变化较小,其间浅层土壤含水量对气温升高更具敏感性.在全球各地多年冻土区的研究发现,气温升高可能会使浅层土壤含水量上升,原因可能是气温升高使土壤冻结锋面逐渐下移,导致固态的冻结水融化为液态水以及降水向下运移[8,34],另外由于高寒草甸及高寒草原具有发达的根系,浅层土壤层的持水能力大,导致土壤含水量上升[34].但当气温升高至一定幅度时,土壤蒸发以及植被蒸腾强度增大,大部分的降水通过植被蒸腾和土壤蒸发逸散到大气中,只有少量的降水在重力作用下运移到下层土壤,可能会导致活动层土壤含水量减小[41].本文模拟结果显示,在完全融化期间浅层土壤出现短暂的土壤含水量下降趋势,这有可能是由于该时期青藏高原腹地降水多以高频小量的降雨发生,下渗以及迁移导致的土壤水分增量不足以弥补气温升高导致的蒸发以及植被蒸腾耗水,大气直接与活动层浅层土壤连接,浅层土壤受气温变化带来的影响更直接[41]. ...
... [41]. ...
The quantitative analysis of the hydro-thermal dynamic of permafrost active layer effected by precipitation
1
2017
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
降水对多年冻土活动层水热影响定量分析
1
2017
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
Spatial heterogeneity of soil moisture in alpine meadow area of the Qinghai-Xizang Plateau
1
2008
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
青藏高原高寒草甸区土壤水分的空间异质性
1
2008
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
The effects of precipitation on thermal-moisture dynamics of active layer at Beiluhe permafrost region
1
2016
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...
降水对北麓河地区多年冻土活动层水热影响分析
1
2016
... 从图10可知,降水增加引起坡上浅层土壤含水量的增加较深层更明显,而且完全融化期的变化最大,主要因为青藏高原降水主要集中在完全融化期.在高强度的蒸散发环境中,由于深层土壤渗透系数小以及水汽运移和蒸发作用的影响,完全融化时期的高频小型降雨无法入渗到深层土壤,可能是65 cm深度土壤含水量没有明显增加的原因[40-42].与坡上不同的是,坡下各深度土壤含水量对降水增加的响应主要集中在融化初期,并且40 cm深度响应程度最大,65 cm深度响应程度最小,一方面可能是因为坡下植被根系、地下生物量及其分布等因素会对40 cm左右的土壤持水性以及土壤空间结构产生影响,40 cm深度土壤具有较好的储水空间和持水能力,对降水增加的响应规律与表层土壤不同[43];另一方面可能是融化初期土壤水分的相态转换以及土壤不同深度之间的水汽运移造成坡上、坡下土壤含水量变化的差异.降雨或降雪会影响土壤含水量在一定时期的动态变化,但各深度土壤含水量年均值对降水增加的响应不明显,说明在强辐射和强蒸发的环境下蒸散发以及水汽运移作用与降水下渗基本维持土壤含水量的平衡[44]. ...


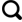



 甘公网安备 62010202000676号
甘公网安备 62010202000676号