Characteristic changes and impacts of permafrost on Qinghai-Tibet Plateau
1
2019
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
青藏高原多年冻土特征、变化及影响
1
2019
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
A new map of permafrost distribution on the Tibetan Plateau
1
2017
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Frozen soil engineering problems in construction of the Qinghai-Tibet Railway
1
2006
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
青藏铁路建设中冻土工程问题
1
2006
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Adaptation methods for transportation infrastructure built on degrading permafrost
0
2016
A review of recent frozen soil engineering in permafrost regions along Qinghai‐Tibet Highway, China
1
2002
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Application of roadbed cooling methods in the Qinghai-Tibet Railway construction
1
2006
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
“冷却路基”方法在青藏铁路上的应用
1
2006
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Natural convection of compressible and incompressible gases in undeformable porous media under cold climate conditions
1
2009
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Comparative analysis of cooling effect of crushed rock embankment along the Qinghai-Tibet Railway
1
2010
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
青藏铁路块石路基冷却降温效果对比分析
1
2010
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Thermo-mechanical stability analysis of cooling embankment with crushed-rock interlayer on a sloping ground in permafrost regions
0
2017
Long-term thermal regimes of the Qinghai-Tibet Railway embankments in plateau permafrost regions
3
2015
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... Material parameters
Table 3| 空气域[10] |
|---|
| 材料 | 导热系数λ/(W·m-1·℃-1) | 比热c/(J·m-3·℃-1) | 密度ρ/(kg·m-3) | 动力黏度μ/(Pa·s) | 膨胀系数β |
| 空气 | 2.0×10-2 | 1.00×103 | 0.64 | 1.75×10-5 | 0.00387 |
| 块石多孔介质域[17] |
| 材料 | 导热系数λf /(W·m-1·℃-1) | 比热cf /(J·m-3·℃-1) | 粒径dp /m | 孔隙率εp | 渗透率k/m2 |
| 块石 | 0.39 | 1.01×106 | 0.25 | 0.47 | 0.39×10-8 |
| 土层域[10] |
| 材料 | 已冻导热系数λf /(W·m-1·℃-1) | 已冻比热cf /(J·m-3·℃-1) | 未冻导热系数λu /(W·m-1·℃-1) | 未冻比热Cu /(J·m-3·℃-1) | 相变潜热L/(J·m-3) |
| 路基填土 | 1.98 | 1.913×106 | 1.92 | 2.227×106 | 2.04×107 |
| 砂土 | 1.65 | 1.825×106 | 1.45 | 2.456×106 | 4.14×107 |
| 粉质黏土 | 1.35 | 1.879×106 | 1.13 | 2.357×106 | 6.03×107 |
| 强风化泥岩 | 1.82 | 1.846×106 | 1.47 | 2.099×106 | 3.77×107 |
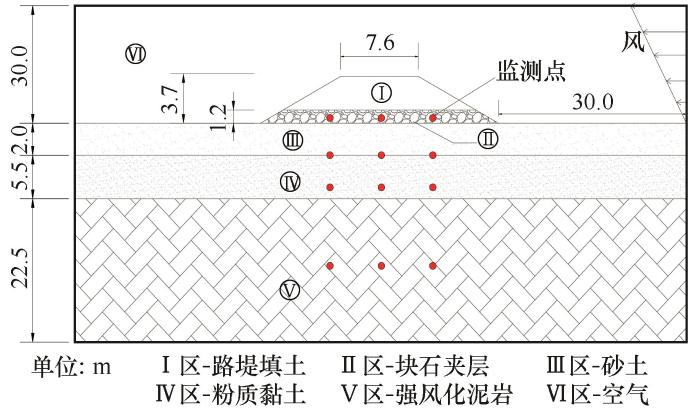
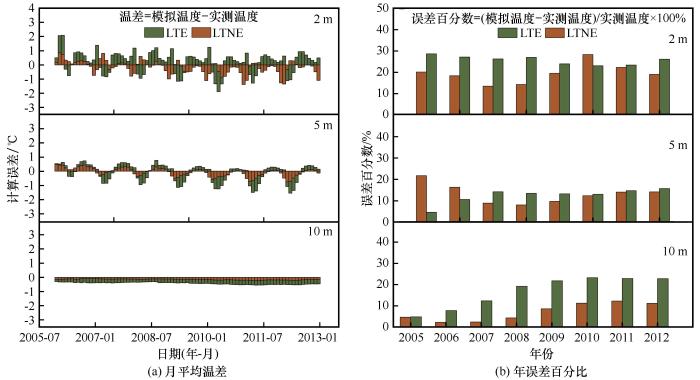
1.4 边界条件考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
... [
10]
| 材料 | 已冻导热系数λf /(W·m-1·℃-1) | 已冻比热cf /(J·m-3·℃-1) | 未冻导热系数λu /(W·m-1·℃-1) | 未冻比热Cu /(J·m-3·℃-1) | 相变潜热L/(J·m-3) |
| 路基填土 | 1.98 | 1.913×106 | 1.92 | 2.227×106 | 2.04×107 |
| 砂土 | 1.65 | 1.825×106 | 1.45 | 2.456×106 | 4.14×107 |
| 粉质黏土 | 1.35 | 1.879×106 | 1.13 | 2.357×106 | 6.03×107 |
| 强风化泥岩 | 1.82 | 1.846×106 | 1.47 | 2.099×106 | 3.77×107 |
1.4 边界条件考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
Study on long-term thermal stability of air-cooled subgrade in permafrost regions
5
2007
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... [
11,
18-
19]
质量方程 | | | 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... [
11]
能量方程 | | | 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... 考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
多年冻土区气冷路基长期热稳定性研究
5
2007
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... [
11,
18-
19]
质量方程 | | | 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... [
11]
能量方程 | | | 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... 考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
Numerical analysis for cooling effect of open boundary ripped-rock embankment on Qinghai-Tibetan Railway
1
2006
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Analysis of non-Darcian effects on temperature differentials in porous media
1
2001
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Porosity of crushed rock layer and its impact on thermal regime of Qinghai-Tibet Railway embankment
1
2017
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Developing thermal flow in open-cell foams
1
2017
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Study of the mechanism of flow and heat transfer on supersonic transpiration cooling
1
2013
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
超声速主流条件发汗冷却的流动和传热机理研究
1
2013
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
Thermal recovery from a fractured medium in local thermal non-equilibrium
2
2013
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... Material parameters
Table 3| 空气域[10] |
|---|
| 材料 | 导热系数λ/(W·m-1·℃-1) | 比热c/(J·m-3·℃-1) | 密度ρ/(kg·m-3) | 动力黏度μ/(Pa·s) | 膨胀系数β |
| 空气 | 2.0×10-2 | 1.00×103 | 0.64 | 1.75×10-5 | 0.00387 |
| 块石多孔介质域[17] |
| 材料 | 导热系数λf /(W·m-1·℃-1) | 比热cf /(J·m-3·℃-1) | 粒径dp /m | 孔隙率εp | 渗透率k/m2 |
| 块石 | 0.39 | 1.01×106 | 0.25 | 0.47 | 0.39×10-8 |
| 土层域[10] |
| 材料 | 已冻导热系数λf /(W·m-1·℃-1) | 已冻比热cf /(J·m-3·℃-1) | 未冻导热系数λu /(W·m-1·℃-1) | 未冻比热Cu /(J·m-3·℃-1) | 相变潜热L/(J·m-3) |
| 路基填土 | 1.98 | 1.913×106 | 1.92 | 2.227×106 | 2.04×107 |
| 砂土 | 1.65 | 1.825×106 | 1.45 | 2.456×106 | 4.14×107 |
| 粉质黏土 | 1.35 | 1.879×106 | 1.13 | 2.357×106 | 6.03×107 |
| 强风化泥岩 | 1.82 | 1.846×106 | 1.47 | 2.099×106 | 3.77×107 |
1.4 边界条件考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
Numerical investigation of local thermal non-equilibrium effects in coal porous media with cryogenic nitrogen injection
2
2018
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
Modeling and simulation of local thermal non-equilibrium effects in porous media with small thermal conductivity
2
2018
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
Numerical investigation of rock-pile based waste heat storage for remote communities in cold climates
4
2019
... 多年冻土约占世界陆地面积的25%,而在我国多年冻土约占国土面积的22.4%,主要分布在青藏高原和东北地区[1-2].青藏高原多年冻土对气候及环境变化敏感,为减少全球气候变暖和工程扰动所导致的融沉病害[3-5],以块石路基为主的“主动冷却路基”[6]因其具有经济,易于施工等优点,可通过调控寒季强迫对流和暖季弱自然对流效应的方式将冷能储存到下伏多年冻土中来实现热防护[7],而被广泛应用于多年冻土路基工程中.对路基温度场的长期监测结果表明,块石结构路基作为一种有效的设计方案,其保持了路基工程完整性并最大限度减少了融沉与冻胀的影响,同时块石基底路基、U型块石路基对下伏多年冻土有着较好的降温效果[8-10].在传统块石结构路基模型传热的计算过程中,考虑了外界风的强迫对流效应,基于连续性方程、非达西流动量方程,以及假设多孔介质中固体骨架和临近孔隙流体温度时时相等的局部热平衡能量方程(LTE),建立出多年冻土区开放块石路基对流换热数值模型[11-12].这类模型的建立为系统评估块石结构长期换热效应奠定了坚实的基础.现有研究结果表明[13],多孔介质的局部热平衡理论的有效性受到流固有效导热系数比(k)、毕渥数(Biot)等一系列参数影响,当多孔介质中流体与固体骨架的热学性质差异逐渐增大时,同一尺度内固体骨架与邻近孔隙流体之间的温差也随之扩大,局部热平衡也将发展为局部非热平衡.青藏铁路块石基底路基所采用的块石粒径约20~30 cm,有效导热系数比可达1/20[14],块石固体骨架与孔隙内部空气之间不可避免地存在一定的温差,局部非热平衡效应不可忽视.在一些多孔介质传热研究过程中均发现了非热平衡效应的存在,如开孔泡沫[15]、烧结金属等微孔隙-小粒径多孔介质内[16],亦或是热干岩储层热回收[17]、液氮对煤矿防火灭火问题[18-19]、废热回收系统[20]等方面,使用LTNE能量方程将使模拟结果精度高于LTE模型.因此,块石这种大孔隙、高渗透率结构内部的局部热非平衡效应如何?在计算块石结构对下部土体热影响时,采用LTNE能量方程相比于传统LTE能量方程的计算精度如何?仍有待进一步研究. ...
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... 通过以上对模拟结果的分析可知,局部非热平衡效应的确存在于块石基底中,其不仅体现在相同时间内块石与空气温度的不相等,也体现二者温度随时间的变化趋势上的差别.两相传热的迟滞效应导致块石的温度变化慢于空气,进而导致了多孔介质中固体与流体的温度不平衡[20]. ...
... 为探求LTNE模型是否可以提高模拟结果的准确性,本节将对开放块石基底路基的模拟过程中同时采用两种多孔介质传热模型进行计算,即LTE与LTNE.在LTNE模型中,使用的换热系数(hsf )由Dixon等[25]在1979年通过理论推导结合试验求得,已有学者在研究加拿大偏远地区岩石废热回收系统时使用该hsf 公式并取得理想结果[20].除此之外,模型的参数保持一致.模拟的结果将与实测值进行对比分析,以证明模拟结果的有效性. ...
Research on the local thermal non-equilibrium effect for heat transfer in porous media
1
2014
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
多孔介质传热局部非热平衡效应的基础问题研究
1
2014
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
Analysis of gaseous slip flow in a porous micro-annulus under local thermal non-equilibrium condition: an exact solution
1
2015
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
Heat and flow characteristics of packed beds
6
1995
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... [23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... [23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... [
23]
| 公式中涉及的重要参数在表2中给出. ...
... Model number and that heat transfer coefficient used
Table 6| 模型序号 | 模型a | 模型b | 模型c | 模型d |
|---|
| 换热系数来源 | Achenbach[23] | Wakao[24] | Dixon等[25] | Pallares等[26] |
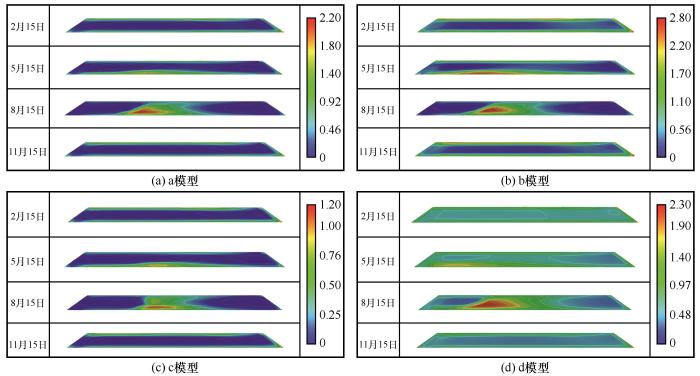
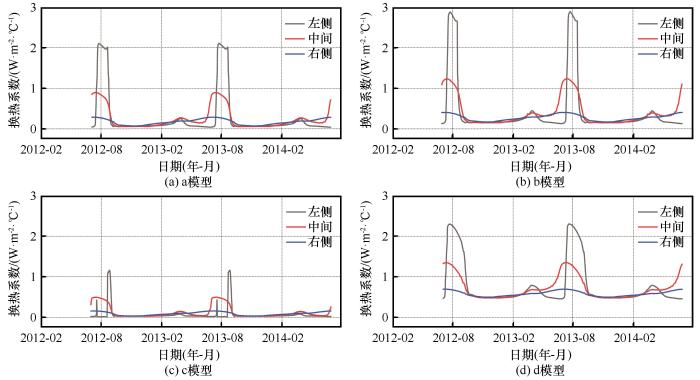
模拟结果显示块石路基中hsf 的值以年为周期呈现规律性波动,根据其变化趋势,提取2014年2月、5月、8月、11月这4个月份的块石路基中hsf 的分布云图(图10).根据云图可以发现块石内部的各个模型hsf 的变化规律相似,在块石路基的边缘位置,即其与路基填土和地表接触处以及与外界空气交汇处hsf 的数值高于块石内部的hsf 数值,这代表在这些区域块石与邻近孔隙空气的能量交换高于其他区域.在一年的大部分时间内,块石路基中的换热处于较为平稳的状态,直到每年的5月,在块石路基中央的底部,hsf 开始增大,直到8月,在路基内部中央靠左的位置上,迎来一年变化的峰值.从图中还可得知,不同模型的hsf 数值大小有所区别.在a、b、c、d四个模型的块石内部,hsf 年平均值分别为0.22、0.35、0.09 W⋅m-2⋅℃-1以及0.68 W⋅m-2⋅℃-1. ...
Particle-to-fluid transfer coefficients and fluid diffusivities at low flow rate in packed beds
4
1976
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... [24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... Model number and that heat transfer coefficient used
Table 6| 模型序号 | 模型a | 模型b | 模型c | 模型d |
|---|
| 换热系数来源 | Achenbach[23] | Wakao[24] | Dixon等[25] | Pallares等[26] |
模拟结果显示块石路基中hsf 的值以年为周期呈现规律性波动,根据其变化趋势,提取2014年2月、5月、8月、11月这4个月份的块石路基中hsf 的分布云图(图10).根据云图可以发现块石内部的各个模型hsf 的变化规律相似,在块石路基的边缘位置,即其与路基填土和地表接触处以及与外界空气交汇处hsf 的数值高于块石内部的hsf 数值,这代表在这些区域块石与邻近孔隙空气的能量交换高于其他区域.在一年的大部分时间内,块石路基中的换热处于较为平稳的状态,直到每年的5月,在块石路基中央的底部,hsf 开始增大,直到8月,在路基内部中央靠左的位置上,迎来一年变化的峰值.从图中还可得知,不同模型的hsf 数值大小有所区别.在a、b、c、d四个模型的块石内部,hsf 年平均值分别为0.22、0.35、0.09 W⋅m-2⋅℃-1以及0.68 W⋅m-2⋅℃-1. ...
Theoretical prediction of effective heat-transfer parameters in packed beds
5
1979
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... [25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... 为探求LTNE模型是否可以提高模拟结果的准确性,本节将对开放块石基底路基的模拟过程中同时采用两种多孔介质传热模型进行计算,即LTE与LTNE.在LTNE模型中,使用的换热系数(hsf )由Dixon等[25]在1979年通过理论推导结合试验求得,已有学者在研究加拿大偏远地区岩石废热回收系统时使用该hsf 公式并取得理想结果[20].除此之外,模型的参数保持一致.模拟的结果将与实测值进行对比分析,以证明模拟结果的有效性. ...
... Model number and that heat transfer coefficient used
Table 6| 模型序号 | 模型a | 模型b | 模型c | 模型d |
|---|
| 换热系数来源 | Achenbach[23] | Wakao[24] | Dixon等[25] | Pallares等[26] |
模拟结果显示块石路基中hsf 的值以年为周期呈现规律性波动,根据其变化趋势,提取2014年2月、5月、8月、11月这4个月份的块石路基中hsf 的分布云图(图10).根据云图可以发现块石内部的各个模型hsf 的变化规律相似,在块石路基的边缘位置,即其与路基填土和地表接触处以及与外界空气交汇处hsf 的数值高于块石内部的hsf 数值,这代表在这些区域块石与邻近孔隙空气的能量交换高于其他区域.在一年的大部分时间内,块石路基中的换热处于较为平稳的状态,直到每年的5月,在块石路基中央的底部,hsf 开始增大,直到8月,在路基内部中央靠左的位置上,迎来一年变化的峰值.从图中还可得知,不同模型的hsf 数值大小有所区别.在a、b、c、d四个模型的块石内部,hsf 年平均值分别为0.22、0.35、0.09 W⋅m-2⋅℃-1以及0.68 W⋅m-2⋅℃-1. ...
A modification of a Nusselt number correlation for forced convection in porous media
3
2010
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
... Governing equation
Table 1| 区域 | 方程类型 | 控制方程 |
|---|
| 空气域[11] | 质量方程 | |
| 动量方程 | |
| 能量方程 | |
| 块石[11,18-19] | 质量方程 | |
| 动量方程 | , |
| 能量方程 | LTE | |
| LTNE | |
| 土层域[11] | 能量方程 | |
| 换热系数 | Achenbach[23] | |
| Wakao[24] | |
| Dixon等[25] | |
| Pallares等[26] | |
| 比表面积[23] | |
公式中涉及的重要参数在表2中给出. ...
... Model number and that heat transfer coefficient used
Table 6| 模型序号 | 模型a | 模型b | 模型c | 模型d |
|---|
| 换热系数来源 | Achenbach[23] | Wakao[24] | Dixon等[25] | Pallares等[26] |
模拟结果显示块石路基中hsf 的值以年为周期呈现规律性波动,根据其变化趋势,提取2014年2月、5月、8月、11月这4个月份的块石路基中hsf 的分布云图(图10).根据云图可以发现块石内部的各个模型hsf 的变化规律相似,在块石路基的边缘位置,即其与路基填土和地表接触处以及与外界空气交汇处hsf 的数值高于块石内部的hsf 数值,这代表在这些区域块石与邻近孔隙空气的能量交换高于其他区域.在一年的大部分时间内,块石路基中的换热处于较为平稳的状态,直到每年的5月,在块石路基中央的底部,hsf 开始增大,直到8月,在路基内部中央靠左的位置上,迎来一年变化的峰值.从图中还可得知,不同模型的hsf 数值大小有所区别.在a、b、c、d四个模型的块石内部,hsf 年平均值分别为0.22、0.35、0.09 W⋅m-2⋅℃-1以及0.68 W⋅m-2⋅℃-1. ...
Internal heat transfer coefficients in microporous media with rarefaction effects
1
2012
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
Analysis of variants within the porous media transport models
1
2000
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
Research on heat and mass transfer with local thermal non-equilibrium in porous media
1
2018
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
多孔介质内局部非热平衡热质传递研究
1
2018
... 如图1所示,与假设多孔介质内部同一时间流固温度局部相等的热平衡理论有所区别,局部非热平衡理论认为多孔介质中的固体骨架与孔隙流体存在一定温差(Ts ≠Tf )并因此发生能量传递(qsf ),而该能量传递由LTNE能量方程中的重要参数流固换热系数(hsf )与比表面积a控制[21].在多孔介质中,固体骨架温度与流体温度通常并非时刻相等.LTE作为LTNE的一种理想状态[22],在流固温度相差不大时使用LTE理论进行数值模拟可以有效精简计算量.因此当我们使用LTNE理论进行多孔介质的传热计算时,准确求得ahsf 的表达式至关重要.科研人员[23-26]已对此展开丰富的研究并求得了一些经典的hsf 表达式,对多孔介质局部非热平衡模型试验的研究作出重要的贡献.Xu等[27]研究了微小多孔介质中微尺度效应对hsf 的影响,发现hsf 随粒径(dp )的减小和努塞尔数的增大而减小.Alazmi等[28]研究发现LTNE模型中不同hsf 之间的差异并不大,通常在进口区域和实验不确定性范围内更为明显.但对于小孔隙度和低雷诺数的情况,Achenbach[23]的求得的换热系数与Wakao[24]和Dixon等[25]求得的换热系数有所不同.路朗[29]在研究低导热系数多孔介质换热时,采用了Achenbach[23]所求得换热系数公式,而在高导热系数多孔介质换热过程中采用了Wakao[24]所求得换热系数公式;而Amiri等[20]在研究高孔隙率-大粒径岩石组成的废热回收填充床中,采用了Dixon等[25]求得的换热系数公式.尽管前人已对各换热系数进行了一定对比分析,但是仍然缺少针对类似块石路基一类的大粒径、高孔隙率的多孔介质内部不同hsf 系统性的对比与分析,以及会对多孔介质内部传热产生何种影响. ...
Long-term cooling effect of the crushed rock structure embankments of the Qinghai-Tibet Railway
2
2019
... 本文基于多孔介质局部非热平衡理论,以北麓河非正线试验段开放块石基底路基信息为依托[30],通过数值模拟并结合一定量监测数据的方法,建立出块石基底路基局部热平衡和局部非热平衡数值模型,探求存在于块石层的随季节更替的局部非热平衡效应、分析LTE、LTNE模型的模拟结果中路基下部土体的温度变化趋势,以及LTNE模型内不同hsf 在块石基底中的变化趋势及其对下部土体温度变化的影响.旨在建立出影响因素更全面的块石结构路基传热模型,从而更合理有效的预测青藏高原冻土路基的温度演化趋势,对于今后块石路基热质传递理论的研究起到积极的推动作用. ...
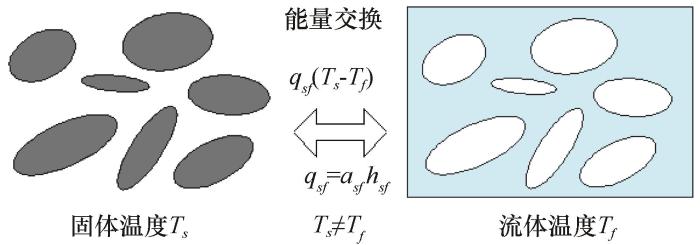
... 本文根据青藏铁路北麓河非正线试验段块石基底路基为原型进行建模[30].模型尺寸信息、土层分布及监测点布置方式如图2所示.路基顶面以及底面的宽度分别为7.6 m和18.7 m,路基高度为3.7 m,坡度为1∶1.5,块石层厚度为1.2 m.下伏土体从上至下分别为砂土、粉质黏土、强风化泥岩,其厚度分别为2.0 m、5.5 m以及22.5 m.通过仿真软件对瞬态计算结果记录、提取的功能实现“监测”的目的,在进行计算之前,首先通过在仿真软件中输入坐标的方式在块石夹层的左侧、中心和右侧布置监测点,其次在监测功能接口中设置不同的需要监测的变量后可获得瞬态计算结果中每个时间节点的多孔介质内流体温度、固体温度以及换热系数的变化趋势.与此同时,通过使用与上述相同的方法在块石层内三个监测点的正下方,地表以下2 m、5 m以及10 m处也相应设置了监测点,用于监测下伏多年冻土的温度变化趋势. ...
1
2002
... 考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
1
2002
... 考虑气候变暖影响,假设青藏高原在未来50年内平均气温将升高2.6 ℃[31],为精简模拟过程的计算量,根据附面层理论以及北麓河地区环境实测温度,本文使用的温度边界条件为基于实测温度拟合而成的温度正弦曲线[图3(a)].可以看出整体上实测温度与拟合温度有着较好的契合性.但由于实际温度受环境因素影响存在一定程度波动,因此拟合得出的正弦形式的温度曲线与以天为单位测得的实测温度相比仍存在一定程度的误差.如图3(b)所示,可以发现在每年温度达到最高的7月以及最低的1月时间段内,拟合温度的误差偏高,其平均值在3.5~4.0 ℃之间,而在其他月份误差较低,平均值为2.69 ℃.北麓河地区的环境的风速变化规律可通过正弦函数表示,同时依据“综合幂次律”理论,环境中的风速随高度增加产生变化,模型右侧边界的风速可近似由指数形式描述.此外,在模型最底部,设置一个热流边界,其代表更深的土体带给模型底部的能量[11].具体边界条件在表4~5中列出,其中,A为年平均温度,B为温度变化幅值,在各个边界处的取值如表5所示. ...
Mechanism of cooling effect of block-stone sandwich subgrade structure on Qinghai-Tibet Railway
1
2007
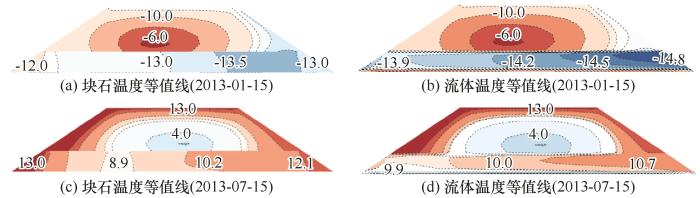
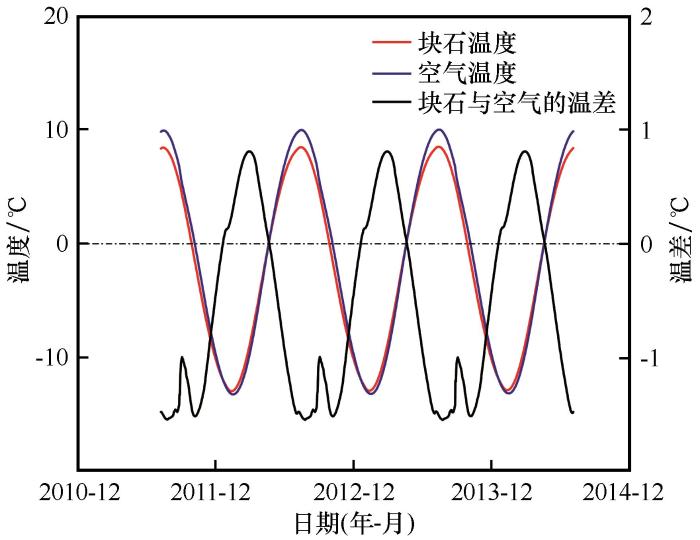
... 由于两个计算域同时存在于块石路基中,在同一监测点上也可以同时读取到两个计算域的模拟结果.图6给出了LTNE模型中块石路基中心位置监测点上多孔介质块石固体骨架和空气随时间变化的温度曲线,以及二者的温差.可以看出,空气的温度变化幅度大于块石,且块石温度变化相比于空气存在一定的迟滞效应.一年内,二者的温度在两个时间点达到相同水平,分别为12月底以及4月底.在4—12月期间,空气温度高于块石,最大温差为1.54 ℃;而在其他时间段,块石温度高于空气温度,最大温差达到0.80 ℃.二者在夏季的温差大于冬季.文献[32-33]中指出,受风速和风向的影响,块石路基以冬半年通风为主的强迫对流与夏半年传导为主的自然对流对多年冻土进行保护,且夏季块石路基顶底板的温差大于冬季.这与模拟得出的结论相同. ...
青藏铁路块石夹层路基结构的冷却作用机理
1
2007
... 由于两个计算域同时存在于块石路基中,在同一监测点上也可以同时读取到两个计算域的模拟结果.图6给出了LTNE模型中块石路基中心位置监测点上多孔介质块石固体骨架和空气随时间变化的温度曲线,以及二者的温差.可以看出,空气的温度变化幅度大于块石,且块石温度变化相比于空气存在一定的迟滞效应.一年内,二者的温度在两个时间点达到相同水平,分别为12月底以及4月底.在4—12月期间,空气温度高于块石,最大温差为1.54 ℃;而在其他时间段,块石温度高于空气温度,最大温差达到0.80 ℃.二者在夏季的温差大于冬季.文献[32-33]中指出,受风速和风向的影响,块石路基以冬半年通风为主的强迫对流与夏半年传导为主的自然对流对多年冻土进行保护,且夏季块石路基顶底板的温差大于冬季.这与模拟得出的结论相同. ...
Monitoring and analysis of cooling effect of block-stone embankment for Qinghai-Tibet Railway
1
2005
... 由于两个计算域同时存在于块石路基中,在同一监测点上也可以同时读取到两个计算域的模拟结果.图6给出了LTNE模型中块石路基中心位置监测点上多孔介质块石固体骨架和空气随时间变化的温度曲线,以及二者的温差.可以看出,空气的温度变化幅度大于块石,且块石温度变化相比于空气存在一定的迟滞效应.一年内,二者的温度在两个时间点达到相同水平,分别为12月底以及4月底.在4—12月期间,空气温度高于块石,最大温差为1.54 ℃;而在其他时间段,块石温度高于空气温度,最大温差达到0.80 ℃.二者在夏季的温差大于冬季.文献[32-33]中指出,受风速和风向的影响,块石路基以冬半年通风为主的强迫对流与夏半年传导为主的自然对流对多年冻土进行保护,且夏季块石路基顶底板的温差大于冬季.这与模拟得出的结论相同. ...
青藏铁路块石路基结构的冷却效果监测分析
1
2005
... 由于两个计算域同时存在于块石路基中,在同一监测点上也可以同时读取到两个计算域的模拟结果.图6给出了LTNE模型中块石路基中心位置监测点上多孔介质块石固体骨架和空气随时间变化的温度曲线,以及二者的温差.可以看出,空气的温度变化幅度大于块石,且块石温度变化相比于空气存在一定的迟滞效应.一年内,二者的温度在两个时间点达到相同水平,分别为12月底以及4月底.在4—12月期间,空气温度高于块石,最大温差为1.54 ℃;而在其他时间段,块石温度高于空气温度,最大温差达到0.80 ℃.二者在夏季的温差大于冬季.文献[32-33]中指出,受风速和风向的影响,块石路基以冬半年通风为主的强迫对流与夏半年传导为主的自然对流对多年冻土进行保护,且夏季块石路基顶底板的温差大于冬季.这与模拟得出的结论相同. ...
Analysis and risk assessment of cooling effect of crushed rock embankment for Qinghai-Tibet Railway under a warming climate
2
2020
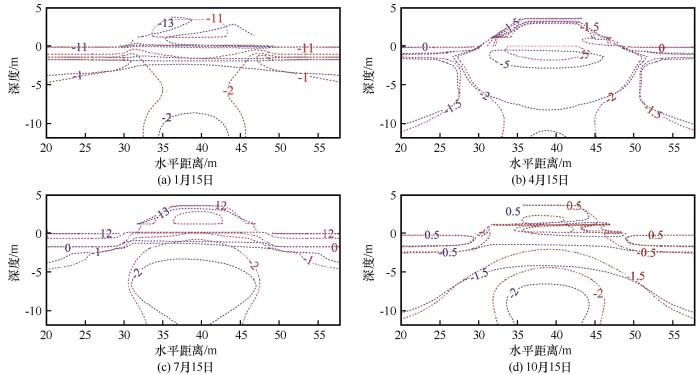
... 研究表明,块石路基下冻土上限往往在4月达到最高,在10月达到最低[34].因此,图7给出了2013年1月、4月、7月、10月共4个月份两个模型的模拟结果中,块石路基以及下部土体温度等值线图,其中蓝色等值线代表LTE模型的温度,红色等值线代表LTNE模型温度.由图可知,10月15日,冻土上限达到一年之内最低,此时块石路基模型的土体温度从上至下降低,且LTE模型的土体温度高于LTNE模型:在此期间,同为-1.5 ℃、-2.0 ℃等值线,LTE模型的等值线位置低于LTNE模型[图7(d)];而在4月15日,冻土上限达到最高,土体温度从上至下升高,LTE模型中-5 ℃、-2 ℃等值线所覆盖区域大于LTNE模型,在此时LTE模型土体温度整体低于LTNE模型[图7(b)].由此可知,土层与块石路基之间的能量交换高于LTNE模型,这导致LTE模型中土体温度受环境温度影响比LTNE模型大. ...
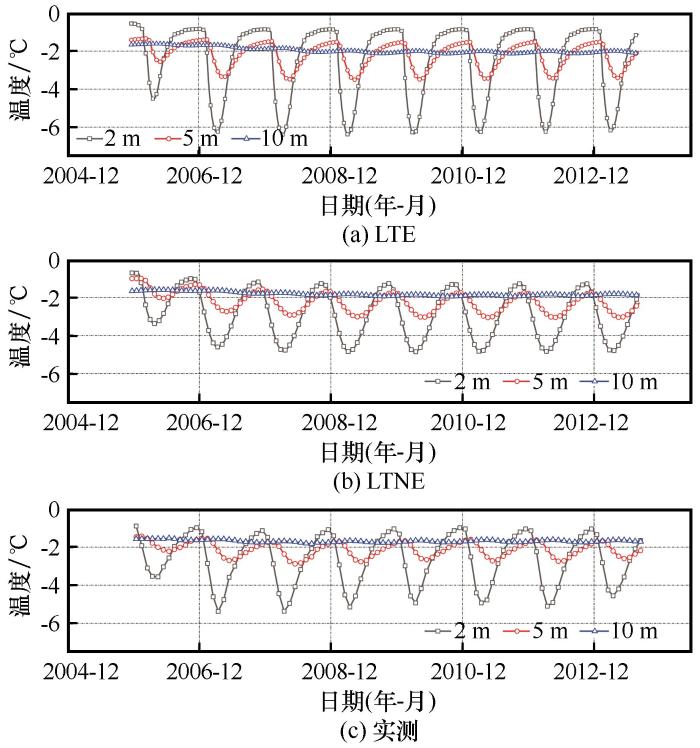
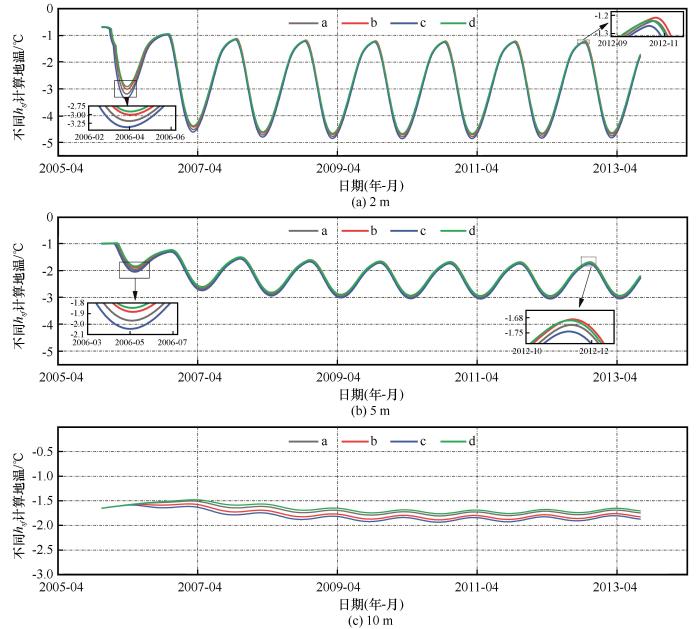
... 如图8所示,考虑到实测值在2005年12月—2013年6月较为完整,模拟结果也截取相同时间段的土体2 m、5 m以及10 m深度的中央监测点处土体温度随时间变化趋势.在路基建成的前几年内(2004—2007年)为快速降温的阶段,两种模型的模拟结果显示在不同深度处均存在一定程度的降温趋势[34].其中,地表以下2 m和5 m处的温度随着季节气温变化而产生明显的周期性波动,而在地表以下10 m处,温度波动幅度受气温变化影响则明显变小.在2005—2006年间,LTE模型在2 m、5 m、10 m三处的年平均地温分别下降了0.73 ℃、0.42 ℃、0.04 ℃;LTNE模型则分别下降了0.85 ℃、0.56 ℃、0.05 ℃;而实测分别下降0.34 ℃、0.28 ℃、0.08 ℃.在此之后,路基的快速降温阶段结束,土体的降温幅度变小,趋于稳定.2007—2011年,LTE模型在三个深度的降温趋势为0.01、0.03、0.04 ℃·a-1;LTNE模型为0.04、0.07、0.04 ℃·a-1.除此之外可以发现,LTE模型在各个深度的土体温度的波动幅度都比LTNE模型大.以拥有全年完整实测温度的最后一个年份(2012年)为例,在地表以下2 m处,LTE、LTNE模型的最低温度为 -6.18 ℃、-4.82 ℃,最高温达到-0.87 ℃、-1.26 ℃;在5 m处,二者最低温度达到了-3.46 ℃、-2.88 ℃,最高温为-1.51 ℃、-1.67 ℃;而在10 m处,二者最低温度达到了-2.13 ℃、-1.91 ℃,最高为 -1.99 ℃、-1.82 ℃.在2012全年,LTE模型在三个土层深度的地温波动幅值分别比LTNE模型大1.75 ℃、0.74 ℃以及0.05 ℃. ...
气候变暖影响下青藏铁路块石结构路基降温效果分析与风险评估
2
2020
... 研究表明,块石路基下冻土上限往往在4月达到最高,在10月达到最低[34].因此,图7给出了2013年1月、4月、7月、10月共4个月份两个模型的模拟结果中,块石路基以及下部土体温度等值线图,其中蓝色等值线代表LTE模型的温度,红色等值线代表LTNE模型温度.由图可知,10月15日,冻土上限达到一年之内最低,此时块石路基模型的土体温度从上至下降低,且LTE模型的土体温度高于LTNE模型:在此期间,同为-1.5 ℃、-2.0 ℃等值线,LTE模型的等值线位置低于LTNE模型[图7(d)];而在4月15日,冻土上限达到最高,土体温度从上至下升高,LTE模型中-5 ℃、-2 ℃等值线所覆盖区域大于LTNE模型,在此时LTE模型土体温度整体低于LTNE模型[图7(b)].由此可知,土层与块石路基之间的能量交换高于LTNE模型,这导致LTE模型中土体温度受环境温度影响比LTNE模型大. ...
... 如图8所示,考虑到实测值在2005年12月—2013年6月较为完整,模拟结果也截取相同时间段的土体2 m、5 m以及10 m深度的中央监测点处土体温度随时间变化趋势.在路基建成的前几年内(2004—2007年)为快速降温的阶段,两种模型的模拟结果显示在不同深度处均存在一定程度的降温趋势[34].其中,地表以下2 m和5 m处的温度随着季节气温变化而产生明显的周期性波动,而在地表以下10 m处,温度波动幅度受气温变化影响则明显变小.在2005—2006年间,LTE模型在2 m、5 m、10 m三处的年平均地温分别下降了0.73 ℃、0.42 ℃、0.04 ℃;LTNE模型则分别下降了0.85 ℃、0.56 ℃、0.05 ℃;而实测分别下降0.34 ℃、0.28 ℃、0.08 ℃.在此之后,路基的快速降温阶段结束,土体的降温幅度变小,趋于稳定.2007—2011年,LTE模型在三个深度的降温趋势为0.01、0.03、0.04 ℃·a-1;LTNE模型为0.04、0.07、0.04 ℃·a-1.除此之外可以发现,LTE模型在各个深度的土体温度的波动幅度都比LTNE模型大.以拥有全年完整实测温度的最后一个年份(2012年)为例,在地表以下2 m处,LTE、LTNE模型的最低温度为 -6.18 ℃、-4.82 ℃,最高温达到-0.87 ℃、-1.26 ℃;在5 m处,二者最低温度达到了-3.46 ℃、-2.88 ℃,最高温为-1.51 ℃、-1.67 ℃;而在10 m处,二者最低温度达到了-2.13 ℃、-1.91 ℃,最高为 -1.99 ℃、-1.82 ℃.在2012全年,LTE模型在三个土层深度的地温波动幅值分别比LTNE模型大1.75 ℃、0.74 ℃以及0.05 ℃. ...


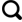





 甘公网安备 62010202000676号
甘公网安备 62010202000676号