Advances in extremes statistics and their application to climate change study
1
2011
... 极端降水是全球最受关注、影响最大的自然灾害之一,是短期气候预测研究的重点[1].IPCC[2]曾指出,随着全球气候变暖,内陆地区的极端降水事件频率呈现出增加趋势.近年来,区域性洪水、干旱、高温、雨雪冰冻等极端事件频发,尤其是20世纪80年代以后,频繁的极端事件给生态环境、经济发展和人民生活造成了严重影响[3-4].因此,研究区域性极端降水事件对科学认识气候变化背景下水循环的时空演变,把握气候异常对极端降水的影响规律,评估水资源管理及区域水资源安全具有十分重要的理论和实践意义. ...
极值统计理论的进展及其在气候变化研究中的应用
1
2011
... 极端降水是全球最受关注、影响最大的自然灾害之一,是短期气候预测研究的重点[1].IPCC[2]曾指出,随着全球气候变暖,内陆地区的极端降水事件频率呈现出增加趋势.近年来,区域性洪水、干旱、高温、雨雪冰冻等极端事件频发,尤其是20世纪80年代以后,频繁的极端事件给生态环境、经济发展和人民生活造成了严重影响[3-4].因此,研究区域性极端降水事件对科学认识气候变化背景下水循环的时空演变,把握气候异常对极端降水的影响规律,评估水资源管理及区域水资源安全具有十分重要的理论和实践意义. ...
2
2001
... 极端降水是全球最受关注、影响最大的自然灾害之一,是短期气候预测研究的重点[1].IPCC[2]曾指出,随着全球气候变暖,内陆地区的极端降水事件频率呈现出增加趋势.近年来,区域性洪水、干旱、高温、雨雪冰冻等极端事件频发,尤其是20世纪80年代以后,频繁的极端事件给生态环境、经济发展和人民生活造成了严重影响[3-4].因此,研究区域性极端降水事件对科学认识气候变化背景下水循环的时空演变,把握气候异常对极端降水的影响规律,评估水资源管理及区域水资源安全具有十分重要的理论和实践意义. ...
... 雅鲁藏布江发源并流经西藏高原,地理位置特殊,是世界上海拔最高的大河之一,平均海拔4 000 m以上,是全球气候主要变化区与敏感区.流域沿岸为西藏主要农、牧业生产区,其洪涝和干旱的频繁发生导致了水资源分布不均,进而影响了流域的用水矛盾和生态环境的恶化,而极端事件的发生是对区域气候、环境变化的重要响应.目前对气候极值进行定量评估的方法以气候动力模式为主,从概率论角度对极端气候事件及可预测性研究并不多,尤其是预测方法.IPCC报告中特别强调统计方法对极端气候事件的重要性[2],因此,本文基于广义帕累托方法(GPD)的分布参数模型,针对超出阈值的数据作为样本数据来建模,从气候极值的分布规律出发,揭示极端降水的发生发展规律,探索极端降水的可预测性,从而更好地预估极端事件,为提高防灾减灾能力提供科学依据. ...
1
2001
... 极端降水是全球最受关注、影响最大的自然灾害之一,是短期气候预测研究的重点[1].IPCC[2]曾指出,随着全球气候变暖,内陆地区的极端降水事件频率呈现出增加趋势.近年来,区域性洪水、干旱、高温、雨雪冰冻等极端事件频发,尤其是20世纪80年代以后,频繁的极端事件给生态环境、经济发展和人民生活造成了严重影响[3-4].因此,研究区域性极端降水事件对科学认识气候变化背景下水循环的时空演变,把握气候异常对极端降水的影响规律,评估水资源管理及区域水资源安全具有十分重要的理论和实践意义. ...
The influence of aggravated global warming on the probability of extreme climatic event
1
2007
... 极端降水是全球最受关注、影响最大的自然灾害之一,是短期气候预测研究的重点[1].IPCC[2]曾指出,随着全球气候变暖,内陆地区的极端降水事件频率呈现出增加趋势.近年来,区域性洪水、干旱、高温、雨雪冰冻等极端事件频发,尤其是20世纪80年代以后,频繁的极端事件给生态环境、经济发展和人民生活造成了严重影响[3-4].因此,研究区域性极端降水事件对科学认识气候变化背景下水循环的时空演变,把握气候异常对极端降水的影响规律,评估水资源管理及区域水资源安全具有十分重要的理论和实践意义. ...
全球变暖加剧对极端气候概率影响的初步探讨
1
2007
... 极端降水是全球最受关注、影响最大的自然灾害之一,是短期气候预测研究的重点[1].IPCC[2]曾指出,随着全球气候变暖,内陆地区的极端降水事件频率呈现出增加趋势.近年来,区域性洪水、干旱、高温、雨雪冰冻等极端事件频发,尤其是20世纪80年代以后,频繁的极端事件给生态环境、经济发展和人民生活造成了严重影响[3-4].因此,研究区域性极端降水事件对科学认识气候变化背景下水循环的时空演变,把握气候异常对极端降水的影响规律,评估水资源管理及区域水资源安全具有十分重要的理论和实践意义. ...
Trends in total precipitation and frequency of daily precipitation extremes over China
1
2005
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
1960-2014年淮河流域极端气温和降水时空变化特征
0
2017
Spatial and temporal variation of extreme precipitation indices in Southwestern China in the rain season
0
2019
中国西南部区域雨季极端降水指数时空变化特征
0
2019
Spatial-temporal variation of extreme precipitation events in Henan province from 1961 to 2013
1
2018
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
1961—2013年河南省极端降水事件时空变化特征
1
2018
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Observed coherent changes in climatic extremes during the second half of the twentieth century
1
2002
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Variations and statistical probability characteristic analysis of extreme precipitation events under climate change in Haihe River Basin, China
1
2014
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Application of generalized Pareto distribution to the research of extreme rainfall of Chongqing
1
2008
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
广义帕雷托分布在重庆暴雨强降水研究中的应用
1
2008
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Extreme precipitation experimentation over eastern China based on generalized Pareto distribution
1
2009
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
利用广义帕雷托分布拟合中国东部日极端降水的试验
1
2009
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Frequency analysis of extreme precipitation in Heihe River basin based on generalized Pareto distribution
1
2014
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
基于GPD分布的黑河流域极端降水频率特征分析
1
2014
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Frequency analysis of the 7-8 December 2010 extreme precipitation in the Panama Canal Watershed
1
2013
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Projected climate change under the RCPs scenario in the Qinghai Plateau
1
2015
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
RCPs情景下未来青海高原气候变化趋势预估
1
2015
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Analysis on climate change of the Qinghai-Tibet Plateau in the recent 50 years
1
2012
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
近50年青藏高原气候变化特征分析
1
2012
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Trends in daily temperature and precipitation extremes over the Yarlung Zangbo River basin during 1961—2005
1
2009
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
近45年雅鲁藏布江流域极端气候事件趋势分析
1
2009
... 极端气候事件归根到底是气候极值问题,气候极值是极端事件产生的必要条件,极端事件发生发展的预测首先要考虑极值的分布规律.国内外部分学者研究表明,中国西部的极端降水天数呈增加趋势,尤其是西北地区[5-8].Fischer等[9]分析了珠江的极端降水分布特征,并估算了极端降水指数.Hong等[10]认为海河流域的极端降水主要发生在38° N,大部分站点的降水呈现出减少趋势.程炳岩等[11]、江志红等[12]研究认为广义帕累托分布函数(generalized Pareto distribution,GPD)在重庆、中国东部的日降水模拟中具有更高的拟合度;李占玲等[13]基于GPD函数分析了黑河流域的极端降水频率特征,得出该流域20世纪60年代发生的极端降水次数最多,90年代以后次数较少.Eylon等[14]运用极值理论分析了巴拿马运河的极端降水分布特征,并估算了极端降水的重现期及相应的置信区间.刘彩红等[15]运用CMIP5模式指出,青海高原的降水有极端化的趋势,极端降水频次增加,强度增大.韩国军[16]、游庆龙等[17]运用统计方法计算出青藏高原极端降水大部分呈增加趋势,且逐年平均降水强度和逐年连续降水天数均有所增加,90年代以来增加明显. ...
Tail index estimation, Pareto quantile plots, and regression diagnostics
1
1996
... GPD可以直接利用历年的原始数据,人为设置阈值,在设置好阈值后,以此为标准来抽取每一年超过此阈值的极大或极小值,即“超门限峰值POT”(peaks over threshold),可以提高估算精度[18].具体为: ...
A simple general approach to inference about the tail of a distribution
1
1975
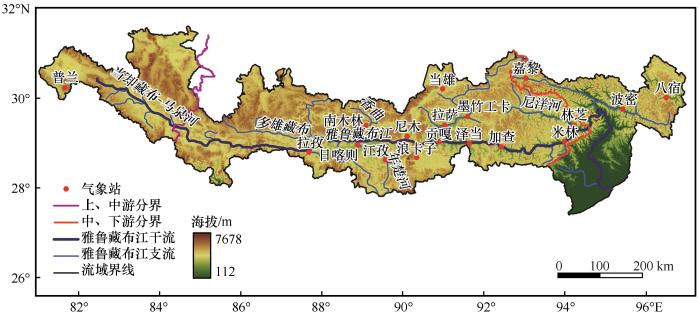
... Hill图法是基于Hill估计量的一种阈值图形法[19],由点(k,1/H(k,n))构成的曲线,通过观察图中尾部指数稳定的区域来选择阈值.其定义为: ...
Analysis and simulation of extreme flow events at Yichang station under climate change
1
2011
... 对GPD分布进行参数估计的方法有很多,本文主要通过极大似然估计法对参数进行估计.该方法具有很强的灵活性,可以适应不同模型的需求, 且统计特性良好,能够综合各种有关信息到统计推断中去.模型估计时,样本变异可能会导致模型参数的不确定性,由于极大似然方法具有渐进正态性, 容易给出估计值及其标准误差(标准误差是参数不确定性或变异性的度量之一).该方法唯一的缺点是计算时迭代繁琐.具体方法见文献[20]. ...
1
1999
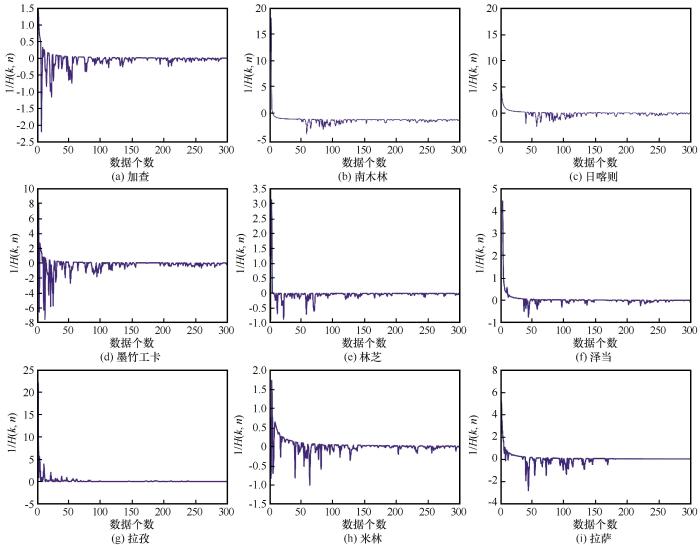
... GPD拟合需要超阈值数据序列满足平稳性的条件,因此,拟合之前需对超阈值序列进行稳定性检验.文章中使用Mann-Kendall(M-K检验)对序列的变化趋势和突变点进行检验.M-K检验[21]是气象学、气候学中经常用来进行突变检验的一种非参数检验方法,它不要求样本符合一定的分布.即给定显著性水平α=0.05,则统计量的临界值为±1.96.统计量大于0,表示序列呈上升趋势;反之, 表明呈下降趋势, 大于或小于±1.96,表示上升或下降趋势明显.该方法能有效区分某一自然过程是处于自然波动还是存在确定的变化趋势,常用于气候变化影响下的降水、干旱频次趋势检测. ...
1
1999
... GPD拟合需要超阈值数据序列满足平稳性的条件,因此,拟合之前需对超阈值序列进行稳定性检验.文章中使用Mann-Kendall(M-K检验)对序列的变化趋势和突变点进行检验.M-K检验[21]是气象学、气候学中经常用来进行突变检验的一种非参数检验方法,它不要求样本符合一定的分布.即给定显著性水平α=0.05,则统计量的临界值为±1.96.统计量大于0,表示序列呈上升趋势;反之, 表明呈下降趋势, 大于或小于±1.96,表示上升或下降趋势明显.该方法能有效区分某一自然过程是处于自然波动还是存在确定的变化趋势,常用于气候变化影响下的降水、干旱频次趋势检测. ...
Temporal and spatial distribution of extreme of extreme precipitation events in Tibet during
1
2014
... 尺度参数主要是描述极值分布的变率,尺度参数越大,极值波动范围越大,表明打破极端降水的记录值也越大.整体而言,雅江流域的尺度参数由下游向上游是逐渐减小的,平均值为5.95.由表3可知,下游地区的尺度参数最大,约为7.00,表明这一区域的极端降水变化幅度很大.从气候背景来看,该地区位于高原季风区,受印缅槽和西风带影响,季节性降水较大[22-23],5—9月的降水总量可达600 mm,是西藏地区夏季降水量最大的区域,因此可能出现的破极端降水记录值要高于其他地区.尺度参数最小的区域位于流域中上游地区,受地理位置和大气环流影响,雨期短,降水量少,且连续降水日数也少,降水极值的范围比较小,区域打破极端降水的记录值要比下游地区低.这与前人研究结果一致[24],我国的干旱地区大部分位于非季风区,降水极值范围较小,破纪录的可能性较季风区小. ...
1961-2010年西藏极端降水事件时空分布特征
1
2014
... 尺度参数主要是描述极值分布的变率,尺度参数越大,极值波动范围越大,表明打破极端降水的记录值也越大.整体而言,雅江流域的尺度参数由下游向上游是逐渐减小的,平均值为5.95.由表3可知,下游地区的尺度参数最大,约为7.00,表明这一区域的极端降水变化幅度很大.从气候背景来看,该地区位于高原季风区,受印缅槽和西风带影响,季节性降水较大[22-23],5—9月的降水总量可达600 mm,是西藏地区夏季降水量最大的区域,因此可能出现的破极端降水记录值要高于其他地区.尺度参数最小的区域位于流域中上游地区,受地理位置和大气环流影响,雨期短,降水量少,且连续降水日数也少,降水极值的范围比较小,区域打破极端降水的记录值要比下游地区低.这与前人研究结果一致[24],我国的干旱地区大部分位于非季风区,降水极值范围较小,破纪录的可能性较季风区小. ...
Diurnal variation characteristics of GPS-Retrieved precipitable water vapor over Mid-East Xizang in summer
2
2016
... 尺度参数主要是描述极值分布的变率,尺度参数越大,极值波动范围越大,表明打破极端降水的记录值也越大.整体而言,雅江流域的尺度参数由下游向上游是逐渐减小的,平均值为5.95.由表3可知,下游地区的尺度参数最大,约为7.00,表明这一区域的极端降水变化幅度很大.从气候背景来看,该地区位于高原季风区,受印缅槽和西风带影响,季节性降水较大[22-23],5—9月的降水总量可达600 mm,是西藏地区夏季降水量最大的区域,因此可能出现的破极端降水记录值要高于其他地区.尺度参数最小的区域位于流域中上游地区,受地理位置和大气环流影响,雨期短,降水量少,且连续降水日数也少,降水极值的范围比较小,区域打破极端降水的记录值要比下游地区低.这与前人研究结果一致[24],我国的干旱地区大部分位于非季风区,降水极值范围较小,破纪录的可能性较季风区小. ...
... 形状参数作为模型的第二个重要参数,不同的形状有不同的尾部分布特征,它表示该区域极端降水的破纪录率.由表3看出,形状参数正值区主要位于拉孜地区,这些地区发生破纪录降水事件的可能性比其他地区大.正是由于该区域降水日数少, 所以一旦有降水过程,就可能会打破降水极值.而下游地区的形状参数为负值,说明这些区域的降水发生破纪录的概率偏小.因为夏季,降雨越频繁的区域,极值变率大,较均值离散程度大,则破纪录的概率较小.有降水的地区,不是有较大的形状参数就是有较大的尺度参数,不可能两个参数都大.形状参数较大的地区,称为“形状参数主导区”,该区域多持续降水,极端气候事件较少;尺度参数较大的区域称为“尺度参数主导区”,该区域降水较少, 且多变, 极端气候事件较多[23]. ...
基于GPS资料分析西藏中东部夏季可降水量日变化特征
2
2016
... 尺度参数主要是描述极值分布的变率,尺度参数越大,极值波动范围越大,表明打破极端降水的记录值也越大.整体而言,雅江流域的尺度参数由下游向上游是逐渐减小的,平均值为5.95.由表3可知,下游地区的尺度参数最大,约为7.00,表明这一区域的极端降水变化幅度很大.从气候背景来看,该地区位于高原季风区,受印缅槽和西风带影响,季节性降水较大[22-23],5—9月的降水总量可达600 mm,是西藏地区夏季降水量最大的区域,因此可能出现的破极端降水记录值要高于其他地区.尺度参数最小的区域位于流域中上游地区,受地理位置和大气环流影响,雨期短,降水量少,且连续降水日数也少,降水极值的范围比较小,区域打破极端降水的记录值要比下游地区低.这与前人研究结果一致[24],我国的干旱地区大部分位于非季风区,降水极值范围较小,破纪录的可能性较季风区小. ...
... 形状参数作为模型的第二个重要参数,不同的形状有不同的尾部分布特征,它表示该区域极端降水的破纪录率.由表3看出,形状参数正值区主要位于拉孜地区,这些地区发生破纪录降水事件的可能性比其他地区大.正是由于该区域降水日数少, 所以一旦有降水过程,就可能会打破降水极值.而下游地区的形状参数为负值,说明这些区域的降水发生破纪录的概率偏小.因为夏季,降雨越频繁的区域,极值变率大,较均值离散程度大,则破纪录的概率较小.有降水的地区,不是有较大的形状参数就是有较大的尺度参数,不可能两个参数都大.形状参数较大的地区,称为“形状参数主导区”,该区域多持续降水,极端气候事件较少;尺度参数较大的区域称为“尺度参数主导区”,该区域降水较少, 且多变, 极端气候事件较多[23]. ...
Simulation on spatial and temporal distribution of precipitation and temperature extremes in China
1
2010
... 尺度参数主要是描述极值分布的变率,尺度参数越大,极值波动范围越大,表明打破极端降水的记录值也越大.整体而言,雅江流域的尺度参数由下游向上游是逐渐减小的,平均值为5.95.由表3可知,下游地区的尺度参数最大,约为7.00,表明这一区域的极端降水变化幅度很大.从气候背景来看,该地区位于高原季风区,受印缅槽和西风带影响,季节性降水较大[22-23],5—9月的降水总量可达600 mm,是西藏地区夏季降水量最大的区域,因此可能出现的破极端降水记录值要高于其他地区.尺度参数最小的区域位于流域中上游地区,受地理位置和大气环流影响,雨期短,降水量少,且连续降水日数也少,降水极值的范围比较小,区域打破极端降水的记录值要比下游地区低.这与前人研究结果一致[24],我国的干旱地区大部分位于非季风区,降水极值范围较小,破纪录的可能性较季风区小. ...
中国降水与温度极值的时空分布规律模拟
1
2010
... 尺度参数主要是描述极值分布的变率,尺度参数越大,极值波动范围越大,表明打破极端降水的记录值也越大.整体而言,雅江流域的尺度参数由下游向上游是逐渐减小的,平均值为5.95.由表3可知,下游地区的尺度参数最大,约为7.00,表明这一区域的极端降水变化幅度很大.从气候背景来看,该地区位于高原季风区,受印缅槽和西风带影响,季节性降水较大[22-23],5—9月的降水总量可达600 mm,是西藏地区夏季降水量最大的区域,因此可能出现的破极端降水记录值要高于其他地区.尺度参数最小的区域位于流域中上游地区,受地理位置和大气环流影响,雨期短,降水量少,且连续降水日数也少,降水极值的范围比较小,区域打破极端降水的记录值要比下游地区低.这与前人研究结果一致[24],我国的干旱地区大部分位于非季风区,降水极值范围较小,破纪录的可能性较季风区小. ...
Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring application
0
2007
Mean and extreme climate change on the Qinghai-Tibetan Plateau with a 2 global warming
1
2015
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...
2 ℃全球变暖背景下青藏高原平均气候和极端气候事件变化
1
2015
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...
Spatio-temporal variation characteristics of extreme precipitation events in Tibet in last 50 years
1
2014
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...
近50年来西藏极端降水时空变化特征
1
2014
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...
Spatio-temporal variation characteristics of extreme precipitation events in Tibet in last 50 years
1
2014
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...
1
2013
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...
1
2013
... 极值模型建立最重要的目的之一就是预测极端事件的重现期或重现水平.如表4所示,根据重现期公式可以得出,从5年一遇和10年一遇的极端降水值来看,雅江流域除拉孜站外,其他地区降雨极值均超过30 mm,日喀则地区的降水极值达50 mm,其中拉萨、泽当、墨竹工卡和南木林站5年一遇和10年一遇的极端降水量分别在40 mm左右.相关研究指出[26-27],当温度上升为2 ℃时,青藏高原的强降水距平百分率平均增多44.5%~59.5%,大值区出现在山南附近,这与我们的研究结论相符合.各站点在15年一遇的极端降水值之后,极值水平的增长变得非常缓慢,其中林芝地区的增长最缓慢,以0.32 mm·a-1的速率增长;日喀则地区的降雨极值增长率最快,约0.72 mm·a-1.西藏地区极端降水频率一般为每年4.3次,强度在20 mm·d-1以上,林芝地区为极端降雨的高值区,且沿雅江一线极端降水的频次呈增加趋势[28-29]. ...


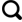



 甘公网安备 62010202000676号
甘公网安备 62010202000676号