A discussion on the boundary and area of the Tibetan Plateau in China
1
2000
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
论青藏高原范围与面积
1
2000
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Dynamic effect of Tibetan Plateau and its impact on weather and climate in China
1
2014
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
青藏高原的动力作用及其对中国天气气候的影响
1
2014
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
The Tibetan Plateau cryosphere: Observations and model simulations for current status and recent changes
2019
Thermal controls on the Asian summer monsoon
1
2012
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Different glacier status with atmospheric circulations in Tibetan Plateau and surroundings
1
2012
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
A new map of permafrost distribution on the Tibetan Plateau
1
2017
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Water recycling between the land surface and atmosphere on the Northern Tibetan Plateau: a case study at ?at observation sites
1
2007
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Investigating soil moisture-climate interactions in a changing climate: A review
1
2010
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Effects of modi?ed soil water-heat physics on RegCM4 simulations of climate over the Tibetan Plateau
1
2016
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
The 40 a variational characteristics of surface heating field over Wudaoliang in the northern Tibetan Plateau
1
2006
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
40年来藏北高原五道梁地区地表加热场的变化特征
1
2006
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Controls of soil organic matter on soil thermal dynamics in the northern high latitudes
1
2019
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Response of boreal ecosystems to varying modes of permafrost degradation
1
2005
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Role of soil freezing in future boreal climate change
1
2004
... 青藏高原平均海拔高度4 000 m以上,在中国境内部分西起帕米尔高原,东至横断山脉,横跨31个经度;南至喜马拉雅山脉南缘,北迄昆仑山-祁连山北侧,纵贯约13个纬度[1].青藏高原以其高大的地形隆升于周围大气之中,其强大的热力和动力作用直接作用于对流层中层,由于其独特的环流特征,青藏高原对亚洲季风的形成和演化具有十分重要的作用,进而对我国乃至全球的气候系统都有着重要的影响[2-4].较高的海拔和独特的地形地貌特征使得青藏高原成为我国冰冻圈的主要分布区[5],其多年冻土总面积约为106万平方公里[6].多年冻土作为气候的产物,气候变化对多年冻土活动层冻融过程有着很大的影响;而与此同时,多年冻土也是气候变化的指示器,土壤温湿度的变化通过改变地表和大气间的能量和水分交换来显著影响当地和东亚的气候系统[7-8].而活动层作为大气与多年冻土之间的纽带,其变化不仅影响自身的水热力性质,而且对水循环[9]、能量交换[10]、碳循环[11]、生态系统[12]及气候系统[13]等都产生重要的影响. ...
Using the NDVI to identify variations in, and responses of, vegetation to climate change on the Tibetan Plateau from 1982 to 2012
1
2017
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Assessment of past, present and future environmental changes on the Tibetan Plateau
1
2015
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
青藏高原环境变化科学评估: 过去、现在与未来
1
2015
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Precipitation over the Tibetan Plateau during recent decades: a review based on observations and simulations
1
2018
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Variations in soil temperature from 1980 to 2015 in permafrost regions on the Qinghai-Tibetan Plateau based on observed and reanalysis products
1
2019
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Frozen soil degradation and its effects on surface hydrology in the northern Tibetan Plateau
1
2015
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Research review on hydrology in the permafrost and seasonal frozen regions
1
2011
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
冻土水文研究进展
1
2011
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Impact of surface energy variation on thawing process within active layer of permafrost
1
2011
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
地表能量变化对多年冻土活动层融化过程的影响
1
2011
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Characteristics of hydro-thermal transfer during freezing and thawing period in permafrost regions
1
2014
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
青藏高原多年冻土区土壤冻融期间水热运移特征分析
1
2014
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Processes of soil thawing-freezing and features of soil moisture migration in the permafrost active layer
1
2014
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
多年冻土区活动层冻融状况及土壤水分运移特征
1
2014
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Simulating the water-heat processes in the permafrost regions in the Tibetan Plateau based on CoupModel
1
2012
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
基于CoupModel的青藏高原多年冻土区土壤水热过程模拟
1
2012
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Heat and water transfer processes on the typical underlying surfaces of frozen soil in cold regions(I): model comparison
2
2013
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
寒区典型下垫面冻土水热过程对比研究(I): 模型对比
2
2013
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
Application of atmospheric model coupled with frozen soil parameterization to simulating spring soil condition in the Qilian Mountains
1
2007
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
耦合冻土方案的大气模式对祁连山区春季土壤状况的模拟
1
2007
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Hydrologic and thermal properties of the active layer in the Alaskan Arctic
1
1991
... 自20世纪以来,以气候变暖为主要特征的全球变化在青藏高原及周边地区表现尤为凸出[14],青藏高原地区升温速率是同期全球升温的两倍以上[15],且降水量不断增加[16].青藏高原气候的不断变暖引发了多年冻土的退化,进而对活动层水热过程产生了影响[17-18].水热过程的改变对于陆气间能量和水分交换、地表感热、潜热输送、水循环过程及生态环境等都会产生重要影响[19].可见,活动层水热变化过程对陆面过程的研究意义较大[20].目前,许多学者针对青藏高原活动层水热变化开展了大量的研究.总的来说,这些研究可以分为两个方面:一类是针对观测站点实测资料的分析[21-22];另一类是使用模型模拟来分析活动层水热过程的变化[23-24].然而青藏高原地区地形复杂,下垫面种类复杂多样,基于实测资料的研究分析虽然能够准确获取活动层水热分布特征,但却因监测站点数目有限,无法开展大范围的研究.因此,模型模拟成为了研究人员较为常用的手段.但是,由于冻融过程中水热过程极为复杂,水分在相变过程中会释放或吸收大量热量,从而影响土壤温度的变化,二者之间相互影响,使得相关研究十分困难[25-26].目前陆面模式中还没有较为合适的土壤水分迁移方案,因此许多模式中关于土壤水分的模拟结果偏差较大,并且大多数模式中还需要输入一些较难获取的土壤质地及下垫面参数信息,这些都给青藏高原地区活动层水热过程的研究带来了困难. ...
Text categorization with KNN algorithm
1
2005
... KNN(K-Nearest Neighbor)算法作为一种信息处理手段,在分类与回归算法领域占有重要的位置,被广泛的应用在机器学习[27]、数据挖掘[28]、文本分类[29]等领域.作为一种用于分类和回归的机器学习算法之一,KNN算法非常有效和易于实现.本研究着眼于青藏高原多年冻土区,基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区活动层表层土壤水热过程进行模拟,并对该模型的模拟效果进行了评估.希望能够对青藏高原多年冻土区水热过程研究提供一种新的研究思路,并为相关研究提供一定的参考. ...
使用KNN算法的文本分类
1
2005
... KNN(K-Nearest Neighbor)算法作为一种信息处理手段,在分类与回归算法领域占有重要的位置,被广泛的应用在机器学习[27]、数据挖掘[28]、文本分类[29]等领域.作为一种用于分类和回归的机器学习算法之一,KNN算法非常有效和易于实现.本研究着眼于青藏高原多年冻土区,基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区活动层表层土壤水热过程进行模拟,并对该模型的模拟效果进行了评估.希望能够对青藏高原多年冻土区水热过程研究提供一种新的研究思路,并为相关研究提供一定的参考. ...
Application of KNN data mining algorithm to haze grade forecasting in Beijing
1
2015
... KNN(K-Nearest Neighbor)算法作为一种信息处理手段,在分类与回归算法领域占有重要的位置,被广泛的应用在机器学习[27]、数据挖掘[28]、文本分类[29]等领域.作为一种用于分类和回归的机器学习算法之一,KNN算法非常有效和易于实现.本研究着眼于青藏高原多年冻土区,基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区活动层表层土壤水热过程进行模拟,并对该模型的模拟效果进行了评估.希望能够对青藏高原多年冻土区水热过程研究提供一种新的研究思路,并为相关研究提供一定的参考. ...
KNN数据挖掘算法在北京地区霾等级预报中的应用
1
2015
... KNN(K-Nearest Neighbor)算法作为一种信息处理手段,在分类与回归算法领域占有重要的位置,被广泛的应用在机器学习[27]、数据挖掘[28]、文本分类[29]等领域.作为一种用于分类和回归的机器学习算法之一,KNN算法非常有效和易于实现.本研究着眼于青藏高原多年冻土区,基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区活动层表层土壤水热过程进行模拟,并对该模型的模拟效果进行了评估.希望能够对青藏高原多年冻土区水热过程研究提供一种新的研究思路,并为相关研究提供一定的参考. ...
Faul tstate perception method for six-phase PMSM based on wavelet neural network and KNN machine learning algorithm
1
2017
... KNN(K-Nearest Neighbor)算法作为一种信息处理手段,在分类与回归算法领域占有重要的位置,被广泛的应用在机器学习[27]、数据挖掘[28]、文本分类[29]等领域.作为一种用于分类和回归的机器学习算法之一,KNN算法非常有效和易于实现.本研究着眼于青藏高原多年冻土区,基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区活动层表层土壤水热过程进行模拟,并对该模型的模拟效果进行了评估.希望能够对青藏高原多年冻土区水热过程研究提供一种新的研究思路,并为相关研究提供一定的参考. ...
基于小波神经网络与KNN机器学习算法的六相永磁同步电机故障态势感知方法
1
2017
... KNN(K-Nearest Neighbor)算法作为一种信息处理手段,在分类与回归算法领域占有重要的位置,被广泛的应用在机器学习[27]、数据挖掘[28]、文本分类[29]等领域.作为一种用于分类和回归的机器学习算法之一,KNN算法非常有效和易于实现.本研究着眼于青藏高原多年冻土区,基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区活动层表层土壤水热过程进行模拟,并对该模型的模拟效果进行了评估.希望能够对青藏高原多年冻土区水热过程研究提供一种新的研究思路,并为相关研究提供一定的参考. ...
The surface energy budget and evapotranspiration in the Tanggula region on the Tibetan Plateau
1
2008
... 本文研究区域选择在青藏高原多年冻土区唐古拉综合观测场(33°04′ N,91°56′ E),海拔高度5 100 m,位于唐古拉山垭口西南部的一个平缓的坡地上,属于典型连续多年冻土区,下垫面类型为高寒草甸,成团簇状,高度较低矮,一年中最高约为10 cm,植被覆盖度约为20%~30%左右[30].其年平均气温为4.9 ℃,极端最高温为17.6 ℃,极端最低温为-29.6 ℃,年平均气压为538 hPa,年均降水量为436.7 mm,降水主要集中在5月至9月,此期间降水量约占全年降水总量的92%,降水强度以小型降水为主[31]. ...
Simulation of the soil water-thermal features within the active layer in Tanggula region, Tibetan Plateau, by using SHAW model
5
2013
... 本文研究区域选择在青藏高原多年冻土区唐古拉综合观测场(33°04′ N,91°56′ E),海拔高度5 100 m,位于唐古拉山垭口西南部的一个平缓的坡地上,属于典型连续多年冻土区,下垫面类型为高寒草甸,成团簇状,高度较低矮,一年中最高约为10 cm,植被覆盖度约为20%~30%左右[30].其年平均气温为4.9 ℃,极端最高温为17.6 ℃,极端最低温为-29.6 ℃,年平均气压为538 hPa,年均降水量为436.7 mm,降水主要集中在5月至9月,此期间降水量约占全年降水总量的92%,降水强度以小型降水为主[31]. ...
... 目前许多陆面模式并不能很好地模拟土壤水分的年变化特征[31,37],KNN模型对表层土壤水分的模拟效果相较于大多陆面模式已有相当程度的提高,今后改善KNN模型对土壤水分模拟效果的工作或许可以从引入额外相关变量、配置适当权重、提高样本量等方面着手. ...
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
... Comparison of correlation coefficients between the model in this paper and other models
Table 2| 深度 | 土壤温度相关系数 | 土壤水分相关系数 |
|---|
| 本研究 | Coupmodel[38] | SHAW[31] | 本研究 | Coupmodel[38] | SHAW[31] |
|---|
| 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
... [
31]
| 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
基于SHAW 模型的青藏高原唐古拉地区活动层土壤水热特征模拟
5
2013
... 本文研究区域选择在青藏高原多年冻土区唐古拉综合观测场(33°04′ N,91°56′ E),海拔高度5 100 m,位于唐古拉山垭口西南部的一个平缓的坡地上,属于典型连续多年冻土区,下垫面类型为高寒草甸,成团簇状,高度较低矮,一年中最高约为10 cm,植被覆盖度约为20%~30%左右[30].其年平均气温为4.9 ℃,极端最高温为17.6 ℃,极端最低温为-29.6 ℃,年平均气压为538 hPa,年均降水量为436.7 mm,降水主要集中在5月至9月,此期间降水量约占全年降水总量的92%,降水强度以小型降水为主[31]. ...
... 目前许多陆面模式并不能很好地模拟土壤水分的年变化特征[31,37],KNN模型对表层土壤水分的模拟效果相较于大多陆面模式已有相当程度的提高,今后改善KNN模型对土壤水分模拟效果的工作或许可以从引入额外相关变量、配置适当权重、提高样本量等方面着手. ...
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
... Comparison of correlation coefficients between the model in this paper and other models
Table 2| 深度 | 土壤温度相关系数 | 土壤水分相关系数 |
|---|
| 本研究 | Coupmodel[38] | SHAW[31] | 本研究 | Coupmodel[38] | SHAW[31] |
|---|
| 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
... [
31]
| 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
1
2003
... 模型模拟的结果好坏可以根据一些统计参数进行评估,相关系数CC(correlation coefficient)和均方根误差RMSD(root-mean-square deviation)是最常用的方法[32].平均偏差MBE(mean bias error)反映的是模拟值与观测值之间的偏离程度,而标准差SD(standard deviation)则代表了一个数据集数据分布的离散程度.这些统计参数的表达式为: ...
Verification of the T213 global spectral model of China National Meteorology Center over the East- Asia area
1
2008
... 式中:、分别为模型预测值与观测值;N为样本容量;分别为模型预测值与观测值的期望值,在这里以其平均值代替.当模型效果理想时,应有CC=1,RMSD=0,SD(X)=SD(Y).根据已有研究,在进行模型效果检验时,当相关系数CC达到0.6时,可以认为模型的预测是成功的[33]. ...
Summarizing multiple aspects of model performance in a single diagram
1
2001
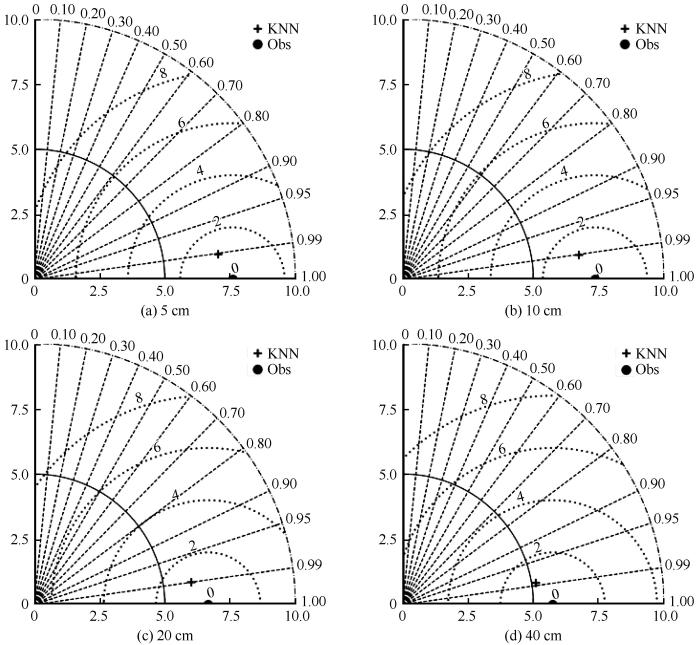
... 泰勒图能够将模型模拟结果与实测数据的标准差、均方根误差和相关系数在一张图上显示出来[34].泰勒图可以比较直观地反映出模型模拟的效果的好坏,在泰勒图上,模拟结果至原点的距离代表了其标准差,方位角的余弦值代表了与观测值的相关系数,模拟结果至观测值之间的距离则代表了两者的均方根误差. ...
Snow-atmosphere coupling and its impact on temperature variability and extremes over North America
1
2017
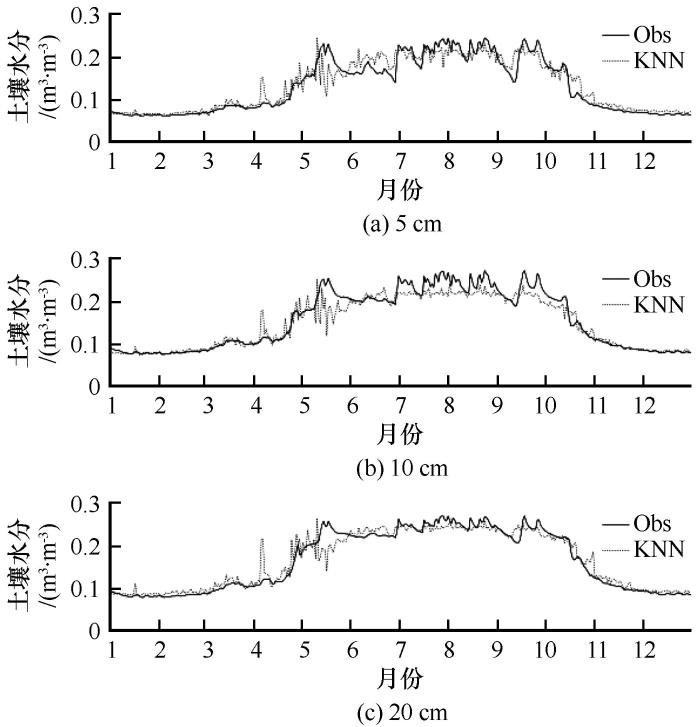
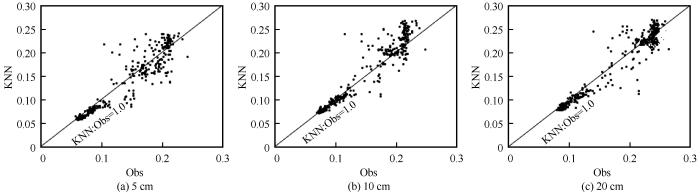
... 多年冻土区活动层土壤水分是陆面过程的重要参量,它对地气热量交换、感热、潜热等都有重要影响,同时也对土壤温度有较大影响,因此,土壤水分的模拟也是陆面过程的重要研究内容[35].图5为不同深度土壤体积含水量模拟值与实测值的对比图,由图中实测土壤水分曲线可以看出,冬春季不同深度土壤水分较低,而夏秋季节土壤水分较高.由春季至夏季,由于温度升高,导致表层土壤逐渐由冻结状态融化成未冻状态产生液态水,冻土的融化与雨季的到来共同造成了表层土壤含水量的逐渐升高[36].夏秋季节,由于降水频繁,导致土壤水分较高,波动较大,这与唐古拉地区雨季区间相符,可见降水对表层土壤水分有较为显著的影响. ...
Processes of soil thawing-freezing and features of soil moisture migration in the permafrost active layer
1
2014
... 多年冻土区活动层土壤水分是陆面过程的重要参量,它对地气热量交换、感热、潜热等都有重要影响,同时也对土壤温度有较大影响,因此,土壤水分的模拟也是陆面过程的重要研究内容[35].图5为不同深度土壤体积含水量模拟值与实测值的对比图,由图中实测土壤水分曲线可以看出,冬春季不同深度土壤水分较低,而夏秋季节土壤水分较高.由春季至夏季,由于温度升高,导致表层土壤逐渐由冻结状态融化成未冻状态产生液态水,冻土的融化与雨季的到来共同造成了表层土壤含水量的逐渐升高[36].夏秋季节,由于降水频繁,导致土壤水分较高,波动较大,这与唐古拉地区雨季区间相符,可见降水对表层土壤水分有较为显著的影响. ...
多年冻土区活动层冻融状况及土壤水分运移特征
1
2014
... 多年冻土区活动层土壤水分是陆面过程的重要参量,它对地气热量交换、感热、潜热等都有重要影响,同时也对土壤温度有较大影响,因此,土壤水分的模拟也是陆面过程的重要研究内容[35].图5为不同深度土壤体积含水量模拟值与实测值的对比图,由图中实测土壤水分曲线可以看出,冬春季不同深度土壤水分较低,而夏秋季节土壤水分较高.由春季至夏季,由于温度升高,导致表层土壤逐渐由冻结状态融化成未冻状态产生液态水,冻土的融化与雨季的到来共同造成了表层土壤含水量的逐渐升高[36].夏秋季节,由于降水频繁,导致土壤水分较高,波动较大,这与唐古拉地区雨季区间相符,可见降水对表层土壤水分有较为显著的影响. ...
Heat and water transfer processes on alpine meadow frozen grounds
1
2010
... 目前许多陆面模式并不能很好地模拟土壤水分的年变化特征[31,37],KNN模型对表层土壤水分的模拟效果相较于大多陆面模式已有相当程度的提高,今后改善KNN模型对土壤水分模拟效果的工作或许可以从引入额外相关变量、配置适当权重、提高样本量等方面着手. ...
黑河高山草甸冻土带水热传输过程
1
2010
... 目前许多陆面模式并不能很好地模拟土壤水分的年变化特征[31,37],KNN模型对表层土壤水分的模拟效果相较于大多陆面模式已有相当程度的提高,今后改善KNN模型对土壤水分模拟效果的工作或许可以从引入额外相关变量、配置适当权重、提高样本量等方面着手. ...
The Water- thermal characteristics of frozen soil under freeze- thaw based on CoupModel
3
2013
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
... Comparison of correlation coefficients between the model in this paper and other models
Table 2| 深度 | 土壤温度相关系数 | 土壤水分相关系数 |
|---|
| 本研究 | Coupmodel[38] | SHAW[31] | 本研究 | Coupmodel[38] | SHAW[31] |
|---|
| 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
... [
38]
SHAW[31] | | 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
基于CoupModel模型的冻融土壤水热耦合模拟研究
3
2013
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
... Comparison of correlation coefficients between the model in this paper and other models
Table 2| 深度 | 土壤温度相关系数 | 土壤水分相关系数 |
|---|
| 本研究 | Coupmodel[38] | SHAW[31] | 本研究 | Coupmodel[38] | SHAW[31] |
|---|
| 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
... [
38]
SHAW[31] | | 5 cm | 0.99 | 0.99 | 0.96 | 0.95 | 0.88 | 0.86 |
| 10 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.91 | 0.79 |
| 20 cm | 0.99 | 0.99 | 0.97 | 0.95 | 0.93 | 0.73 |
| 40 cm | 0.99 | 0.99 | 0.97 | | | |
然而,KNN模型还存在一定的缺陷,主要体现在以下几个方面:首先,该方法需要有一个较长时间段的数据来作为样本进行训练和测试;其次,由于该模型对历史数据有较强的依赖性,无法较好地对极值进行模拟;最后,本文只针对唐古拉地区进行了模型的适用性分析,在其他站点是否能够很好的模拟还有待于进一步的分析验证. ...
Thermal condition of the active layer on the Qinghai-Tibet Plateau simulated by using the model of GIPL2
1
2018
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...
基于GIPL2模型的青藏高原活动层土壤热状况模拟研究
1
2018
... 土壤温湿度的模拟是陆面过程研究的热点,已有多位研究者采用了不同的模型来对青藏高原多年冻土区土壤温湿度进行模拟[24,38].许多学者利用SHAW模型来模拟土壤温度变化特征,然而在SHAW模型中,植被信息、地表反照率等输入变量的的偏差都会对输出结果有很大影响[31].GIPL2模型由于对土壤温度模拟效果较好,同样得到了许多学者的青睐,然而该模型同样需要输入植被类型信息,土壤热导率参数如导热率和体积热容等[39].本研究基于KNN算法,建立了一个气象数据的回归模型,对青藏高原多年冻土区水热过程进行了模拟,并对该模型的模拟效果进行了评估.统计整理有关唐古拉地区水热过程其他陆面模式的模拟结果并同本文的模拟结果进行了比较(表2),可以看出本文对土壤温湿度的模拟效果还是较为理想的.另外,值得注意的是,作为一种新的研究思路,本模型的搭建相比于其他陆面模式来说更为快捷高效,且只需输入较易获得的气象参数,不需要输入研究站点的植被及土壤质地等信息,操作方法简便,运行速度快.这在下垫面类型复杂且缺乏土壤质地等信息的青藏高原地区不失为一种较为理想的方法. ...






 甘公网安备 62010202000676号
甘公网安备 62010202000676号