0 引言
南极冰盖作为世界主要的冷源库之一,不仅为大气纬圈环流提供驱动力,影响着大洋间水汽交换以及热量平衡[1-3],还由于其冰雪表面反照率的变化与气温的正反馈效应进而对全球气候变化产生一定影响[4]。此外,由于南极的淡水储量巨大,气温的升高和表面冰盖的融化会直接影响全球海平面高度和海洋环流[5-8]。另一方面,南极对全球气候变化较为敏感,是全球气候变化的放大镜和重要指示器[9-10],因此对南极的天气气候观测与研究,不但有利于发觉中低纬度地区人类难以捕捉的预警性天气变化,还可以加深我们对全球气候系统的理解,探究过去发生的环境变化并且提高对天气变化预报的水平。然而南极地区气候环境极其恶劣,需要借助人工的实地观测只能在较小的区域进行,大量的冰雪覆盖区域缺乏存档完整且时间序列长的站点[11-12],而遥感卫星产品所提供的观测数据虽然覆盖范围广泛,但时间序列较短[13],因此南极是当前世界上最缺乏现场观测资料的地区之一[14-15]。观测数据的缺乏,不仅增加了目前对南极研究结果的不确定性,还限制了该地区气候特征的表达以及我们对南极气候变化机理的理解。
再分析资料作为一种可以提供较长时间序列且覆盖范围广泛的格网数据,目前已经取得一定的进展。然而再分析资料的质量很大程度上取决于资料同化系统所用观测的质量和数量以及预报模式的性能。此外,Bromwich等[16]发现再分析资料在南半球高纬度地区的趋势被证明存在一定的虚假性。另一方面,针对全球气候模式在高纬度地区模拟的缺陷与难点,研究人员开发了一系列适用于极地的区域气候模式。虽然区域气候模式的强迫场需要在其域的边界提供,而无法对全球气候进行反馈,但是由于区域气候模式的分辨率相对较高,而且在南极大陆进行的观测数量仍然有限,使得高分辨率区域气候模型成为动态缩小全球再分析数据尺度,生成精细尺度气象资料的适当工具[17]。Polar WRF被认为是现如今最先进的极地气候模式之一,Bromwich等[18]、Hines等[19-20]、Listowski等[21]在北极地区进行了一系列测试,结果表明模式的模拟结果较为良好。Bozkurt等[13]比较了南极半岛Polar WRF和RACMO的温度模拟结果,研究显示两者在模拟南极半岛的不同温度状况方面表现出良好的技巧,并且彼此之间有密切的时空变化。马永锋[22]的研究表明,Polar WRF模拟的500 hPa的风向和ERA-interim模拟结果的大气活动中心的位置和强度十分一致,均很好地模拟出了南极大陆上空强大的冷低压。Deb等[23]在西南极地区开展了高水平分辨率的模拟试验,结果表明Polar WRF模式是一个捕捉近地表气象条件的有利工具,在西南极地表气压的模拟方面表现出很高的技巧。此外,Steinhoff等[24]针对南极McMurdo独特的地理环境,通过修改模式中的雪场、土地利用、土壤等的输入,改进了对极端天气的模拟,并首次对该区域的焚风物理机制进行了解释。然而Wilson等[25]对Polar WRF3.1.1的试验结果表明Polar WRF在云微物理过程中存在一定缺陷,从而进一步影响对极地的短波辐射和长波辐射的模拟。总体来看目前测试研究主要集中在北极地区,尽管在南极地区已经展开了一些研究,但是由于计算条件的限制,所有的模拟都只局限在特定的区域[26]。另一方面,已开展的模拟试验中所用的侧边界资料主要以NECP FNL为主,然而马永锋[22]的研究表明NECP FNL在南极地区的整体精度要略低于ERA-interim,且ERA-interim初始和横向边界条件用于南极洲气候降尺度研究[27],与观测结果相比表现良好。所以开展以ERA-interim提供初始场条件的Polar WRF3.9.1的数值模拟研究,对其模拟结果进行分析评估是改进模式的重要前提。本文采用ERA-interim为Polar WRF3.9.1提供风、温度、位势和相对湿度等初始场信息,对南极冰盖2004—2013年的2 m气温、10 m风速以及近地表气压进行模拟,并与28个气象站的观测资料进行对比分析进而评估模式的性能。模式的模拟结果不仅可以弥补极地地区气象站点观测数据缺失,为人们提供长时间序列的气象数据进行科学研究,还可以为模式的完善与改进提供参考依据。
1 模式、数据与方法
1.1 Polar WRF模式和数值试验介绍
Polar WRF是极地气象学小组和俄亥俄州立大学继Polar MM5之后在WRF模式基础上联合开发的更加先进的极地区域气候模式,它是WRF模型的极地版本[28]。Polar WRF在水平方向上求解Arakawa C格网完全可压缩非静水方程组,在垂直方向上采用地形跟随坐标系。该模式对陆面模型中海冰的表示进行了修改,允许指定海冰厚度和积雪深度,而不是仅通过掩模划分海冰是否存在(0表示海冰不存在,1为海冰存在),海冰反照率、海冰厚度和海冰上的积雪不再是固定的,可随季节改变而变化[17-18]。此外模式中的Noah-LSM模型被Hines和Bromwic进行了优化[16],对雪的热特征进行优化并改进热通量计算,并将地表雪的影响应用于模型中,使模型更适用于极地环境。
本文采用模式Polar WRF3.9.1进行数值试验,试验区域差分格式选择Arakawa C跳点格式,并采用极射投影作为投影方式。模拟区域被划分为129×129个格网,格点之间的水平间距为50 km,包括了南纬50°以南的整个区域。模式在垂直方向上采用质量垂直坐标,设置最高层气压为5 000 Pa,最高层与地表面之间共被划分成44个全垂直η层,垂直差值方式为SINT。模式的时间积分步长被设为150 s,实时输入数据时间间隔为6小时,模拟所需的海表温度场、初始土壤参数(土壤水、水分和温度)以及地表气温、气压等初始资料由ERA-interim(6小时,0.75°×0.75°)提供。试验中海冰场的资料和海表温度由再分析资料提供。而土地高程数据和土地覆被信息分别来由默认的分辨率为30弧度的GTOPO30、USGS24类土地覆被资料所提供。模式还采用了分辨率为1°的深层土壤温度数据、基于MODIS精度为30 s的植被指数数据以及精度为0.15°的月地表反照率和雪反照率数据。模式运行采用了以下物理参数化方案:(1)在微物理方案上采用了适用于高分辨率模拟,包括冰、雪、霰等过程的WSM6方案;(2)在辐射方案中采用了新版RRTM长波辐射和Goddard短波辐射方案;(3)在近地层采用了基于Monin-Obukhov相似理论的JanJicEta方案;(4)陆面过程采用了由极地气象小组改进的适用于极地天气的Unified-Noah陆表面模式;(5)在积云参数化过程中采用了基于集合平均方法的New Grell(G3)方案,该方案允许格点的沉降效应向周围传递;(6)在行星边界层参数化中采用了囊括了自由大气中所有湍流状态的MYJ PBL方案。
1.2 数据介绍
1.2.1 气象观测资料
本文所用南极冰盖上的气象观测站点实测资料均来自于南极科学研究委员会(SCAR: Scientific Committee on Antarctic Research)的南极环境研究参考数据(READER: Reference Antarctic Data for Environmental Research)项目。该数据库主要包括三个来源:一是时间比较久远,相关气象观测资料较为匮乏的观测数据,其主要来自于CLIMAT气候数据的月平均;而对较早期的气象观测资料主要通过观测者进行目视读取后借助电传磁带打孔记录;而近期的实时数据则是通过WMO全球电信系统获取,各站点的具体位置分布和绍如表1和图1所示。这些站点中序号为1~11的站点分布在南极半岛,序号为20~28的站点分布在东南极沿岸,剩余的Byrd、Harry、Theresa站位于西南极,Larsen_Ice_Shelf、Amundsen_Scott、Dome_C_II、Vostok、Harry位于东南极内陆地区。
表1 观测站地理位置、高程、观测类型
Table 1
| 序号 | 站名 | 站点类型 | 纬度/S | 经度/E | 高程/m | 格点 | 格点高程/m |
|---|---|---|---|---|---|---|---|
| 1 | Marsh | 人工气象站 | 62.2° | -58.9° | 10 | (94,13) | 36 |
| 2 | Great_Wall | 人工气象站 | 62.2° | -59.0° | 10 | (94,13) | 36 |
| 3 | Jubany | 人工气象站 | 62.2° | -58.6° | 4 | (94,13) | 36 |
| 4 | King_Sejong | 人工气象站 | 62.2° | -58.7° | 11 | (94,13) | 36 |
| 5 | Esperanza | 人工气象站 | 63.4° | -57.0° | 13 | (94,16) | 1 045 |
| 6 | Marambio | 人工气象站 | 64.2° | -56.7° | 198 | (93,18) | 74 |
| 7 | Palmer | 人工气象站 | 64.3° | -64.0° | 8 | (87,15) | 204 |
| 8 | Marble_Point | 自动气象站 | 77.4° | 163.7° | 12 | (38,71) | 255 |
| 9 | Rothera | 人工气象站 | 67.5° | -68.1° | 32 | (81,20) | 51 |
| 10 | San_Martin | 人工气象站 | 68.1° | -67.1° | 4 | (81,21) | 240 |
| 11 | Butler_Island | 自动气象站 | 72.2° | -60.2° | 91 | (82,31) | 27 |
| 12 | Byrd | 自动气象站 | 80.0° | -119.4° | 1 530 | (53,45) | 1 547 |
| 13 | Henry | 自动气象站 | 89.0° | -1.0° | 2 754 | (66,63) | 2 653 |
| 14 | Theresa | 自动气象站 | 77.9° | 166.5° | 20 | (59,69) | 127 |
| 15 | Larsen_Ice_Shelf | 自动气象站 | 66.9° | -60.9° | 17 | (87,21) | 0 |
| 16 | Amundsen_Scott | 人工气象站 | 90.0° | 0° | 2 835 | (64,63) | 2 772 |
| 17 | Dome_C_II | 自动气象站 | 75.1° | 123.4° | 3 280 | (46,89) | 3 235 |
| 18 | Vostok | 人工气象站 | 78.5° | 106.9° | 3 490 | (57,86) | 3 459 |
| 19 | Harry | 自动气象站 | 83.0° | -121.4° | 954 | (56,51) | 971 |
| 20 | Novolazarevskaya | 人工气象站 | 70.8° | 11.8° | 119 | (103,72) | 290 |
| 21 | Syowa | 人工气象站 | 69.0° | 39.6° | 21 | (97,92) | 556 |
| 22 | Mawson | 人工气象站 | 67.6° | 62.9° | 16 | (85,105) | 577 |
| 23 | Zhongshan | 人工气象站 | 69.4° | 76.4° | 18 | (74,105) | 296 |
| 24 | Davis | 人工气象站 | 68.6° | 78.0° | 13 | (73,107) | 140 |
| 25 | Casey | 人工气象站 | 66.3° | 110.5° | 42 | (46,110) | 215 |
| 26 | Dumont_Durville | 人工气象站 | 66.7° | 140.0° | 43 | (26,95) | 373 |
| 27 | Pegasus_North | 自动气象站 | 84.6° | -115.8° | 1 463 | (59,53) | 1 714 |
| 28 | McMurdo | 人工气象站 | 77.9° | 166.7° | 24 | (39,69) | 127 |
图1
1.2.2 再分析资料
本文采用ERA-interim为模式提供运行所需要的近地面气温、平均海表气压、相对湿度、风速风向等驱动数据。ERA-interim是ECMWF借助ERA-40数据同化经验上发布的更为先进的全球气象资料同化数据,其同化系统基于2006年发布的IFS(Cy31r2)。该数据的分辨率在水平方向上为T255(80 km),在垂直方向上从地表至10 Pa分为60层。ERA-interim数据包括自1979—2019年的每日四次(0000、0600、1200和1800 UTC)分析资料和每天两次的10天气象预测资料(初始化时间分别为0000、1200 UTC)。
1.3 方法介绍
为分析Polar WRF3.9.1对南极冰盖的气候模拟能力,本文采用最邻近法将模式结果提取出来与相应站点进行对比分析。
由于海拔高度会对温度、气压产生影响,而模式输出的格网数据的格点值是该格网覆盖区域的平均值,提取的模式结果与对应气象站点的海拔高度并不一致,因而有必要在对比两组数据前对其进行订正,消除由海拔高度不一致带来的误差
通过气温与海拔的关系,对2 m气温的订正如下:
而对地表气压需要依据拉普拉斯压髙公式进行订制,公式如下:
式中:
对风速的计算公式如下:
式中:
本文提取模式结果进行订正后与气象站数据进行了对比,其中采用平均偏差(Bias)、均方根误差(RMSE)、平均绝对误差(MAE)以及相关系数(R)等作为统计参量。上述统计参量的计算公式如下:
式中:
2 结果分析
2.1 2 m气温
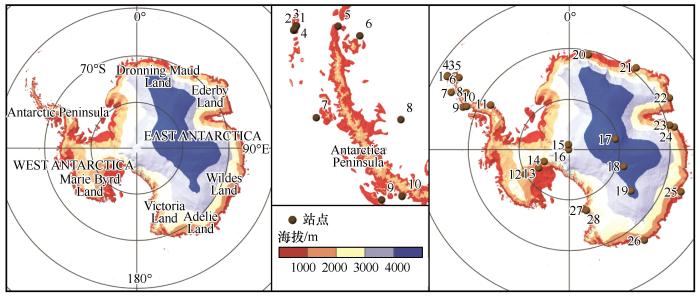
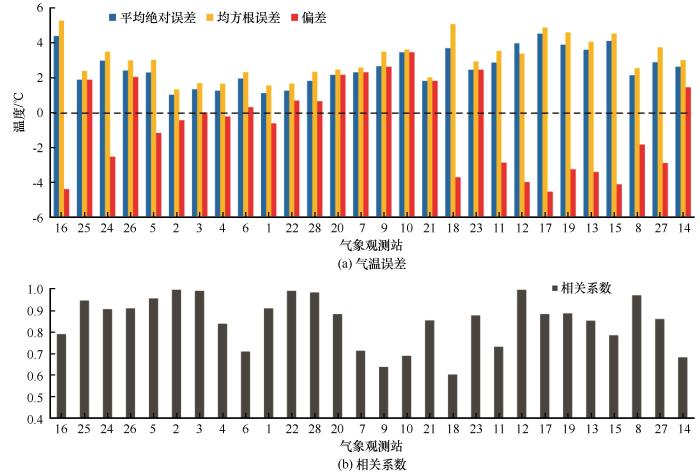
模式模拟年平均2 m气温在各气象站点的具体误差及分布情况如图2~3所示。从各站点均方根误差和平均绝对误差分布来看,Great_wall、Jubany(站点编号2,3)等沿岸站点的误差最小,在2 ℃左右,而位于内陆地区的Amunder、Dome_C_II和Vostok(站点编号16,17,18)等站点年平均气温值与实测值相差较大,在4 ℃左右,其中Amunder和Vostok站均方根误差和平均绝对误差的差异较其他站点要偏高,说明这些站点受极端值影响较大。从所有站点的误差的分布状况可看出,南极沿岸地区的均方根误差和平均绝对误差明显小于南极内陆地区。而分析各站点的偏差可以看出,呈冷偏差与呈暖偏差的站点数大体相同,其中在东南极沿岸除Davis以来其他站点均为冷偏差,整个南极内陆大部分站点均为暖偏差,而在南极半岛既存在冷偏差站点也存在暖偏差站点,且冷暖偏差的站点数大致相同。此外所有站点的模拟年平均气温与实测年平均气温的相关系数都通过了
图2
图2
模式各站点年平均2 m气温误差和相关系数统计
Fig.2
Correlations and differences between simulations and observations for annual average 2 m temperature
图3
图3
年平均2 m气温误差分布
Fig.3
The error spatial distribution of annual average 2 m temperature
图4
图4
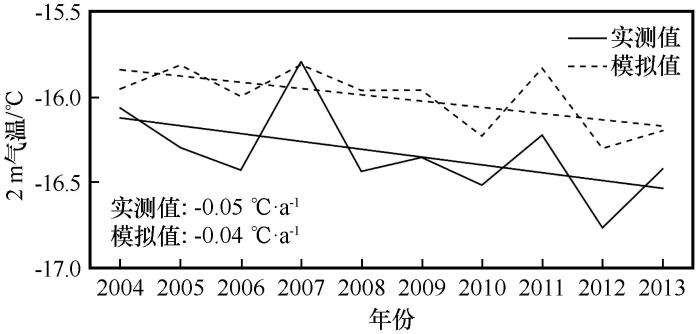
2004—2013年2 m气温模拟值和观测值对比
Fig.4
Comparison of simulated and observed annual mean 2 m temperature during 2004—2013
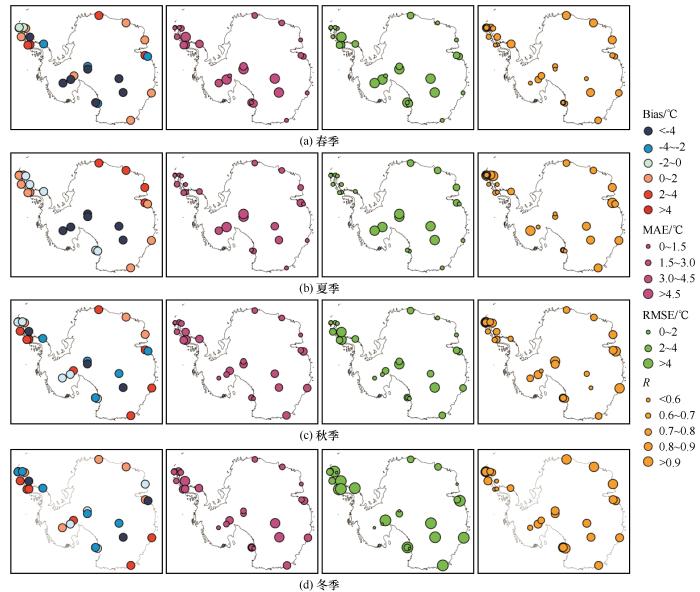
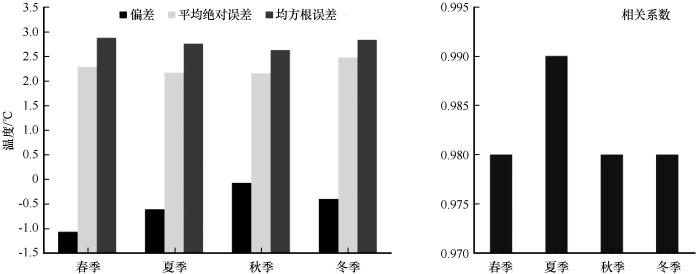
图5为各站点四季模拟误差及相关系数的具体分布状况。比较所有站点的平均绝对误差、均方根误差可看出,东南极沿岸的各站点在四个季节的误差普遍较低,但在秋季和冬季Davis、Dumont_Durville和Casy等站点的误差要高于春季和夏季;南极半岛在夏季所有站点的误差较低,而在春季、秋季和冬季,既存在误差较大的站点也存在误差较小的站点;而在南极内陆,各站点在四个季节均呈现较高的误差,但秋季各站点的整体误差要小于其他三个季节。分析图6可看出,四季的模拟误差均低于3.00 ℃,其中模式对夏季和秋季的模拟误差要低于春季和冬季。而从偏差值的分布来看,东南极沿岸各站点的模拟气温在四季均较实际气温偏冷,南极半岛上较实际气温偏暖和偏冷的站点均存在,而南极内陆均较实际气温偏暖,且暖偏差值较大,说明内陆的系统性误差偏大。比较各站点相关性可发现,四季整体相关性都较为良好,但是在春季和夏季南极半岛和南极内陆部分站点相关性较低,秋季南极半岛和东南极各站点的相关系数都高于0.60,整体相关性要略高于南极内陆,冬季各站点的相关性整体较好,其在南极内陆和东南极罗斯冰架附近站点的相关性要明显高于春季和夏季。统计所有站点四季的2 m气温相关系数,分析可看出四季相关性大致相同,都高于0.97。
图5
图5
四季平均2 m气温误差和相关性数分布
Fig.5
Correlations and differences between simulations and observations for seasonal average 2 m temperature
图6
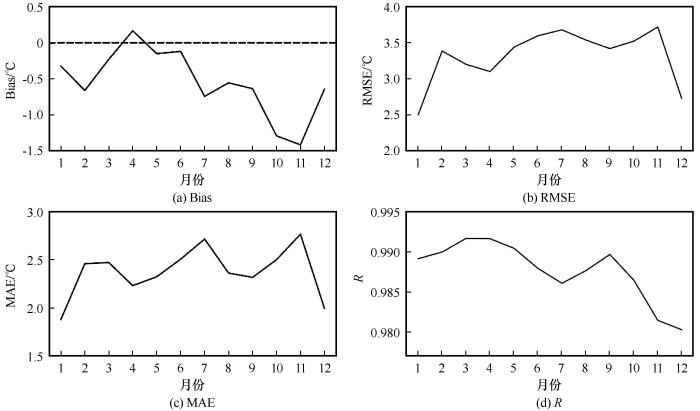
图7是模式和气象数据的月平均气温误差统计。从图中可看出除4月模拟气温略低于实测气温以外,其他月份气温均呈现被高估的状态,其中11月的月偏差值最大约为-1.50 ℃。进一步分析各月份误差可看出,1月、12月模拟误差值最低,均方根误差和平均绝对误差分别约为2.50 ℃、2.00 ℃,7月和11月误差最高,均方根误差和平均绝对误差分别约为5.50 ℃、2.75 ℃。此外统计各月的相关系数可得到12个月份相关系数范围为0.980~0.995,相关性很高,这表明模拟月平均气温与实测月平均气温十分吻合,Polar WRF可以很好地再现南极的月平均气温。
图7
图7
月平均2 m气温模拟值和观测值年内变化和误差统计
Fig.7
Variation and errors between simulated and observed monthly mean 2 m temperature
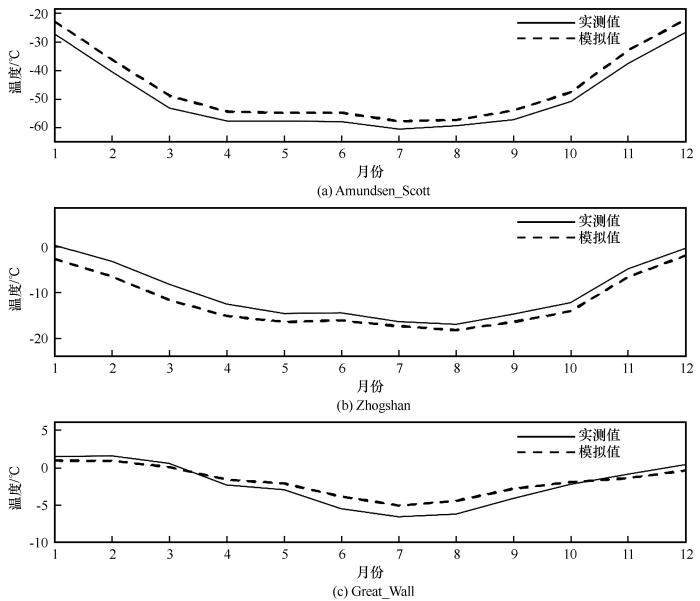
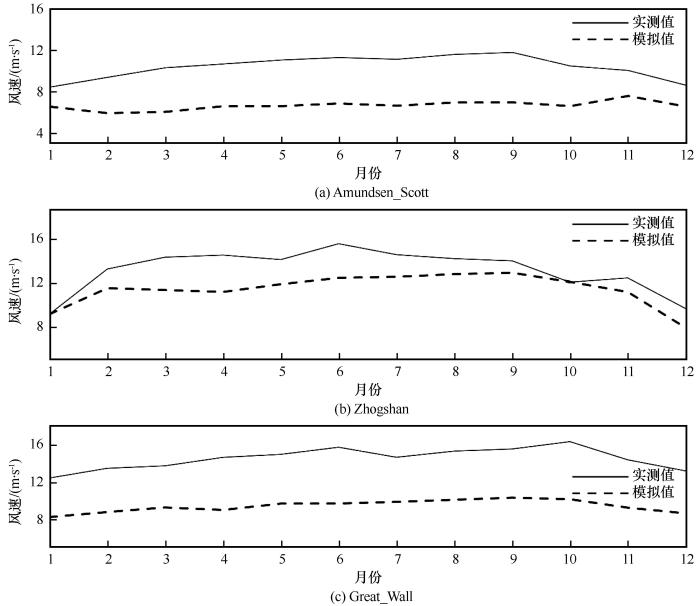
为进一步分析模式的模拟结果,本文选取分别位于南极点、南极半岛、东南极沿岸的Amundsen_Scott、Zhongshan、Great_wall为代表性站点,给出各站点的模拟2 m气温与观测2 m气温的月平均分析结果。如图8所示,Amundsen_Scott在4—9月气温变化曲线十分平缓,表现出了南极大陆地区“无心”现象。Zhongshan、Great_Wall在冬半年整体变化略大,最低气温出现在7、8月。与实测气温相比,Amundsen_Scott站的模拟气温在所有月份都偏高,Zhongshan站的模拟气温在所有月份都偏低,而Great_wall在冬半年(4—10月)的模拟气温偏高,在其余月份模拟气温偏低。而从误差来看,Amundsen_Scott在各月份的误差相差较小,其在12月的误差最大为4.59 ℃,在7月误差最小为1.99 ℃;中山站在5—12月的模拟误差偏小,而在1—4月误差较大,误差范围在2.67~3.38 ℃;Great_wall在1—5月和10—12月误差较小,而在6—9月误差较大,误差范围在1.60 ℃左右。
图8
图8
代表站点月平均2 m气温模拟值和观测值
Fig.8
Simulated and observed monthly mean 2 m temperature in representative stations
2.2 10 m风速
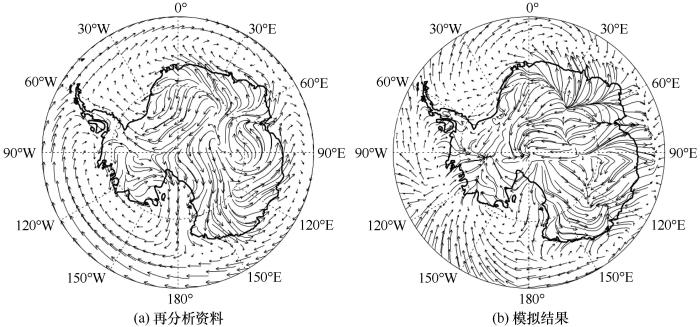
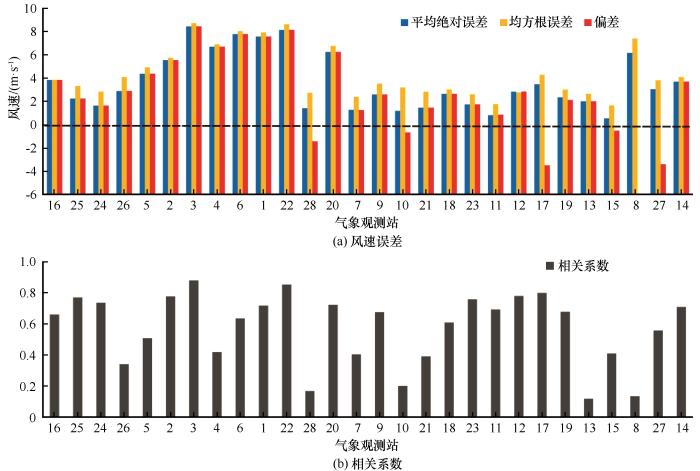
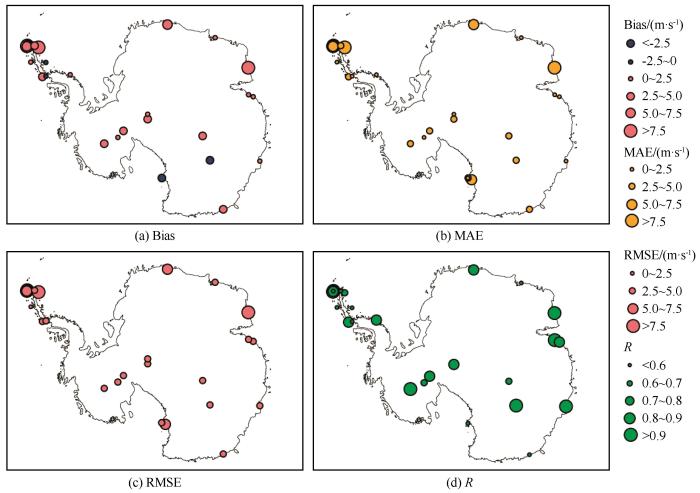
风分为风速与风向,在对风速评估前有必要对风向进行一定的研究,图9给出了再分析资料与模式模拟的10 m风速的分布图。从图中可以看出两者都很好地模拟出了南极大陆的下降风、近海岸绕极涡旋的强度及位置。图10~11给出了所有站点年平均风速的误差及相关系数的大小分布状况。从中可以看出所有站点年平均风速的均方根误差和平均绝对误差的数值范围分别为0.55~8.44 m·s-1、1.65~8.71 m·s-1。与沿岸站点相比,位于内陆的各站点的误差整体较小,均低于5.00 m·s-1;东南极沿岸地区Marble_Point、Novolazarevskay、Mawso等站(站点序号8、20、22)的均方根误差较大,其余站点较小;而在南极半岛各个站点上差异较大,如在Jubany、Marambio (站点序号3、6)的误差均大于7.5 m·s-1,而Larsen_Ice_Shelf (站点序号15)的均方根误差和平均绝对误差仅为1.95 m·s-1、0.75 m·s-1。此外从不同误差指标的差异来看,San_Martin、Syoma、Marble_Point(站点序号10、21、8)的均方根误差要明显高于平均绝对误差,说明这些站点部分年份的误差极值偏大。统计所有站点的正负偏差数可以看出,有82%的站点呈现正偏差(正偏差表示模式结果高估了实测结果),剩余站点呈负偏差,风速整体上以低估为主。从相关性上来看,所有站点模拟值与观测值的相关系数范围为0.30~0.94,86%的站点通过了
图9
图9
再分析资料与模拟结果10 m风向
Fig.9
10 m wind direction from ERA-Interim reanalysis data and Polar WRF simulation
图10
图10
模式年平均10 m风速误差和相关系数统计
Fig.10
Correlations and differences between simulations and observations for annual average 10 m wind speed
图11
图11
年平均10 m风速误差分布
Fig.11
The error spatial distribution of annual average 10 m wind speed
图12
图12
2004—2013年10 m风速模拟值和观测值对比
Fig.12
Comparison of simulated and observed annual 10 m wind speed during 2004—2013
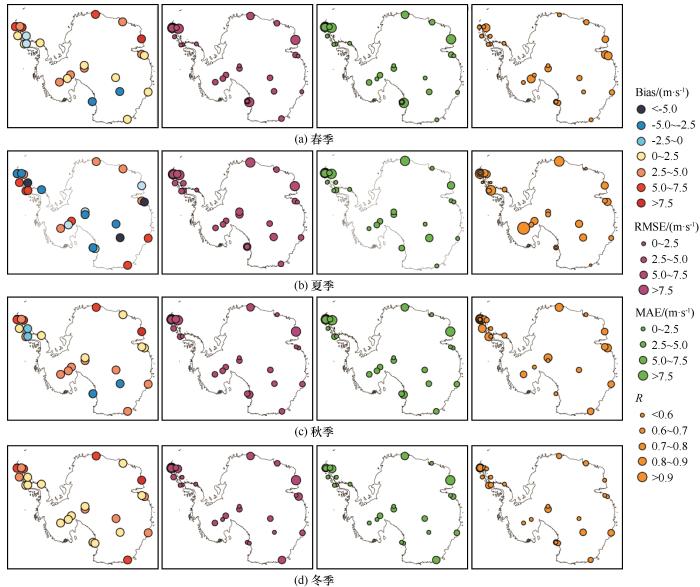
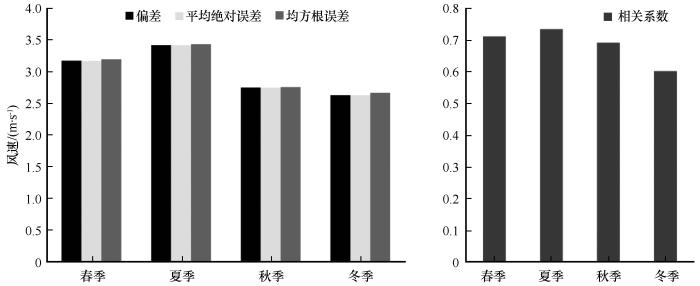
图13为各站点2004—2013年四季模拟风速的误差及相关系数具体分布状况。从误差分布来说,东南极沿岸Novolazarevskaya、Mawson站在四季误差都偏高,Syowa、zhongshan、Dumont_Durville在四季误差都较低,其余站点在不同季节平均误差差异较大;南极半岛上,Jubany、King_Sejong、Marsh、Great_wall在四季误差整体偏高,其余站点在四季误差都较低;而在南极内陆,夏季Larsen_Ice_Shelf、Amundsen_Scott、Harry三个的均方根误差要高于其他三个季节。结合图13来看,模式对10 m风速的模拟在冬季误差最低,其均方根误差和绝对误差分别为2.67 m·s-1、2.63 m·s-1,春季和秋季次之、夏季误差最高,其均方根误差和绝对误差分布为3.42 m·s-1、3.44 m·s-1。比较不同季节各站点偏差值分布可发现,春季和秋季除Henry、Novolazarevskaya、Syowa、Theresa四个站以外其余站点风速均被高估,冬季所有站点的模拟风速均高于实测风速,而夏季风速值被低估的站点数明显多于其他三个季节。而在相关性上来看,东南极沿岸不同站点在四季的相关性差异较大,既存在相关性较高的站点,也存在相关性较低站点;南极半岛在夏季的相关性整体较高,秋季和冬季次之,春季仅Marmbio站点相关性较高,其余站点相关性都偏低;在南极内陆,春季、夏季和秋季的相关性略低,而冬季相关较高,所有站点的相关性都高于0.60。统计2003—2014年四季模拟值与实测值相关性(图14),可以看出模式对整个南极冰盖模拟结果在夏季相关性最高,春季次之,冬季和秋季相关性相对较低。
图13
图13
各站点季节平均10 m风速误差和相关性数分布
Fig.13
Correlations and differences between simulations and observations for seasonal average10 m wind speed
图14
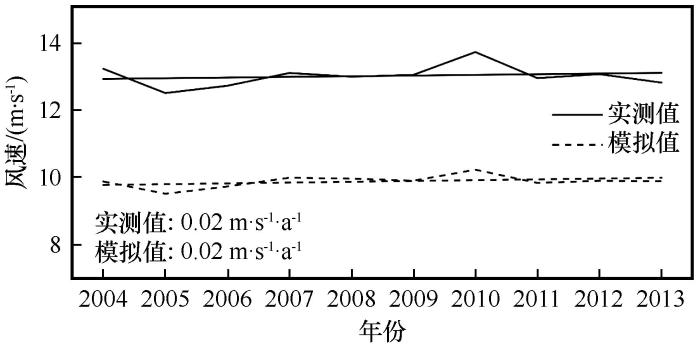
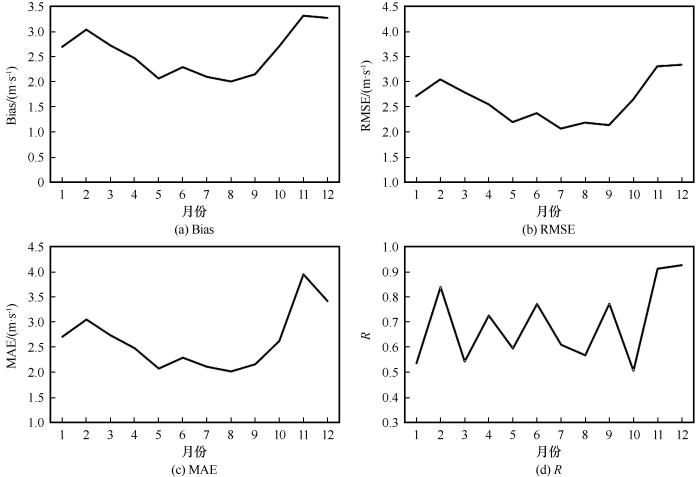
图15给出了模式输出结果和气象观测数据各月的误差统计。从误差分布来看,12个月的偏差、均方根误差和绝对误差范围为2.50~4.50 m·s-1,所有月份均表现为正偏差,即模拟气压高于实际气压。误差自2月到5月不断减小,从6月到9月误差上下波动,其中最小误差出现在7月份,自9月到11月风速误差不断增大,最大误差出现在11月。统计12个月份月平均风速的模拟值与实测值的相关系数可得到,相关性最差和最高的月份分别出现在1月和12月。12个月份相关系数呈上下不断波动状态,2、4、6、9、11、12月相关性较高其余月份相关性较低。整体来看,所有月份的相关系数都超过了0.50且均通过了α=0.1的显著性检验,模拟月平均风速与实测风速较为吻合。
图15
图15
10 m风速月平均模拟值和观测值
Fig.15
Variation and errors between simulated and observed monthly average 10 m wind speed
图16为Amundsen_Scott、Zhongshan、Great_wall三个代表站点的模拟10 m风速与观测10 m风速的月平均分析结果。Amundsen_Scott、Zhongshan、Great_Wall月平均风速值分别在8.46~11.30 m·s-1、9.72~15.62 m·s-1、12.50~16.42 m·s-1,三个站点的最高值分别出现在9月、6月和6月,而最低值均出现在1月和12月。与沿岸相比内陆的风速整体偏低,且风速变化值较为平缓。与实测风速相比,三个站点的模拟风速均低于实测风速,其中位于内陆的Amundsen_Scott在1—2月、10—12月(夏半年)的误差偏小,但在3—9月误差较大;中山站与其他两个站点相比,整体误差偏低,尤其是在1—2月和8—12月;Great_wall的风速值最高,误差也整体高于另外两个站点,各个月份误差大致相同大概在4.21~5.24 m·s-1。
图16
图16
代表站点10 m月平均风速模拟值和观测值
Fig.16
Simulated and observed monthly average 10 m wind speed in representative stations
2.3 近地面气压
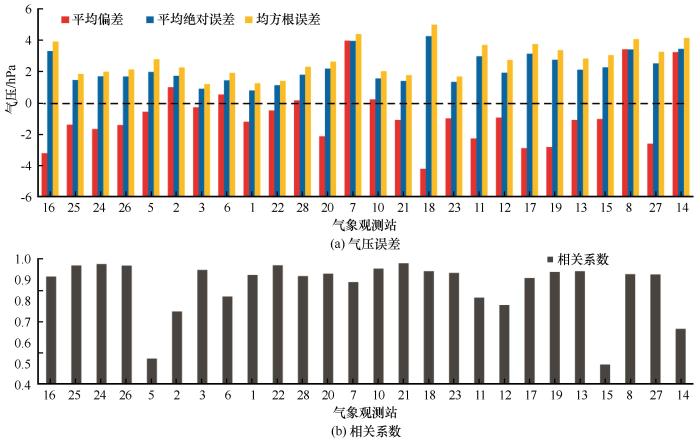
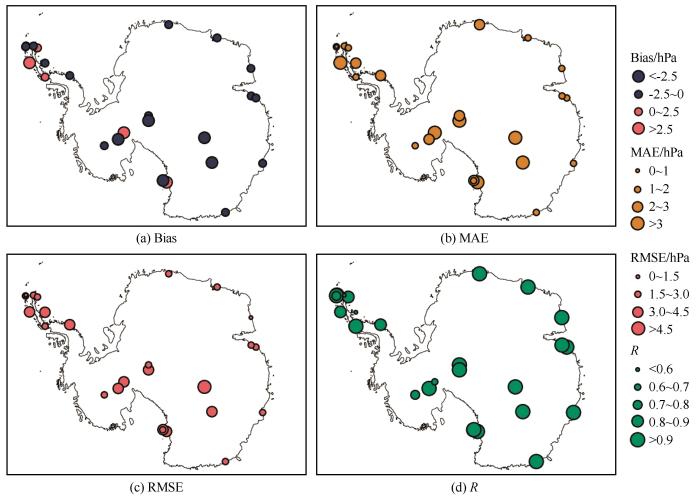
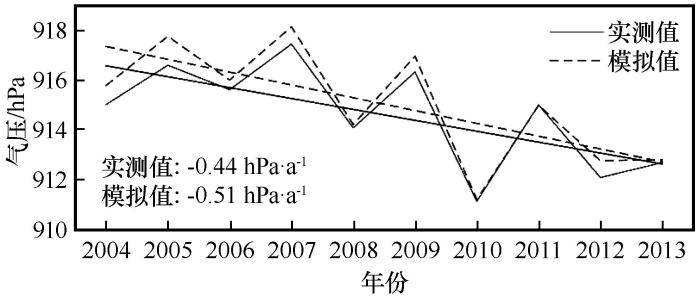
由于King_Sejong和Rother站近地面气压观测数据大量缺失,在验证模式对近地面气压的试验中去除了对这两个站的对比分析。各气象站点模拟误差及分布情况如图17~18所示。所有站点中Vostok站(站点编号18)的均方根误差和平均绝对误差最大,分别为5.00 hPa、4.26 hPa,Jubany站最小(站点编号3),分别1.19 hPa、0.81 hPa。从区域分布来看,东南极沿岸各站点的均方根误差和平均绝对误差较小,仅Pegasus_North(站点编号27)的误差高于3 hPa,南极半岛整体误差略高,但除Palmer站(站点编号7)以外其余站点的误差均小于4 hPa,而和沿岸相比,南极内陆的误差明显偏大,除Byrd站(站点编号12)以外其余站点的误差明显较高。统计所有站点平均偏差可以得到,地表气压的偏差范围在-4.20~3.97 hPa之间,有19个站点为负偏差,7个站点为正偏差,总体而言模式对地面气压整体呈高估状态,其中呈正偏差的站点主要分布在南极半岛和南极内陆。地表气压的模拟值与实测值的相关系数范围为0.50~0.98,其中有81%的站点相关系数大于0.80。所有站点的相关系数都通过了α=0.1的显著性检验,模拟气压与实测气压较为吻合。从相关性分布来看,东南极沿岸所有站点的相关性都高于0.80,相关性很高,而在南极半岛和南极内陆仅有部分站点相关性较低,其余站点相关性都普遍较好。图19对比分析了2003—2014年模拟气压和实测气压整体的年际变化和趋势。与年平均模拟气压相比,Polar WRF模拟气压的年平均值除2011年以外其余年份均偏低。而从两者年变化趋势来看,模拟值和观测值均呈下降趋势,年下降幅度分别为-0.44 hPa·a-1和-0.51 hPa·a-1,模式能够较好呈现气压的年变化趋势。
图17
图17
模式年平均近地面气压精度评估
Fig.17
Correlations and differences between simulations and observations for annual average near surface pressure
图18
图18
年平均近地面气压误差分布
Fig.18
The error spatial distribution of annual average near surface pressure
图19
图19
2004—2013年近地面气压模拟结果和观测值对比
Fig.19
Comparison of simulated and observed annual mean near surface pressure during 2004—2013
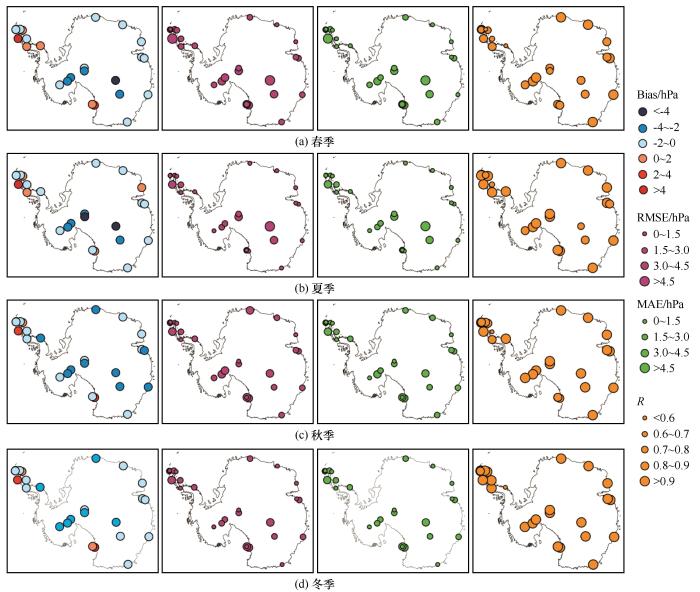
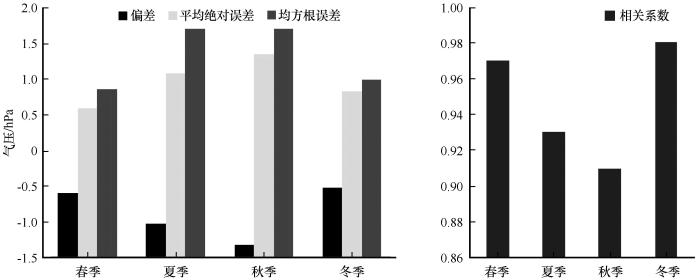
图20为各站点四季模拟近地面气压的精度分布状况。比较所有站点平均绝对误差、均方根误差的分布来看,东南极沿岸的整体误差普遍偏低,在各个季节均要低于南极半岛和南极内陆;南极半岛在春季误差略高,其余三个季节整体误差较小;南极内陆在春、夏、秋三季误差偏高,大于南极半岛,而在冬季其误差略低,与南极半岛相差不大。结合表4来看,模式对近地表气压的模拟精度在冬季最高均方根误差和绝对误差分别为2.00 hPa、1.90 hPa,其次是秋季和夏季,春季的模拟精度最低,均方根误差和绝对误差分别为2.52 hPa、2.22 hPa。从各季节的偏差分布可得到,模式对四个季节近地表气压的模拟主要以高估为主,其中少数模拟气压较实测值偏低的站点主要位于南极沿岸,而位于内陆的各站点模拟气压均被高估。进一步比较不同季节相关性可发现,大部分站点在四个季节的相关性都高于0.6,但是与其他季节相比,春季位于南极半岛上的各站点相关性要略低于其他季节。统计2003—2014年四季模拟气压与实测气压相关性(图21),可以看出模式对气压的模拟在四个季节的相关性都很高,均大于0.9,其中冬季相关性最高,春季和夏季次之,秋季最低。
图20
图20
各站点季节平均近地面气压误差和相关性数分布
Fig.20
Correlations and differences between simulations and observations for seasonal average near surface pressure
图21
图21
四季近地面气压季误差统计
Fig.21
Statistics of seasonal average near surface pressure errors
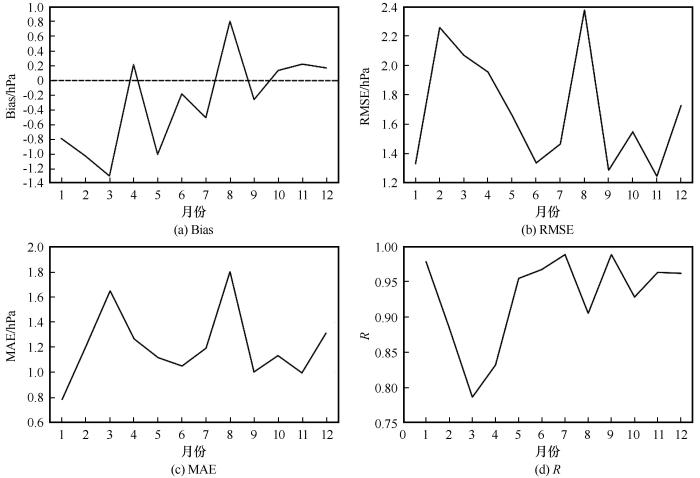
对月平均近地面气压模拟值和观测值进行统计比较,计算不同月份的误差大小和相关系数(图22),进而分析模式对近地表气压在月时间尺度的模拟精度。从图中可看出1—3月、5—7月和9月的模拟气压要高于实测气压,而其他月份气压则被低估,其中3月的月偏差值最低为-1.29 hPa,而8月的月偏差值最高为0.76 hPa。进一步分析均方根误差和平均绝对误差可看出,模拟误差在2—6月不断减小,在6—8月又不断增加,8月误差值达到最大均方根误差和平均绝对误差分别为2.37 hPa、1.80 hPa,随后在8—12月误差呈上下波折趋势。此外统计各月的相关系数可得到12个月份相关系数范围为0.79~0.99,相关性最高和最低月份分别为3月和7月,整体来看所有月份相关性较高且都通过了α=0.05的显著性检验,这表明模拟月平均气温与实测月平均气温吻合性良好。
图22
图22
月平均近地面气压模拟值和观测值年内变化和误差统计
Fig.22
Variation and errors between simulated and observed monthly average near surface pressure
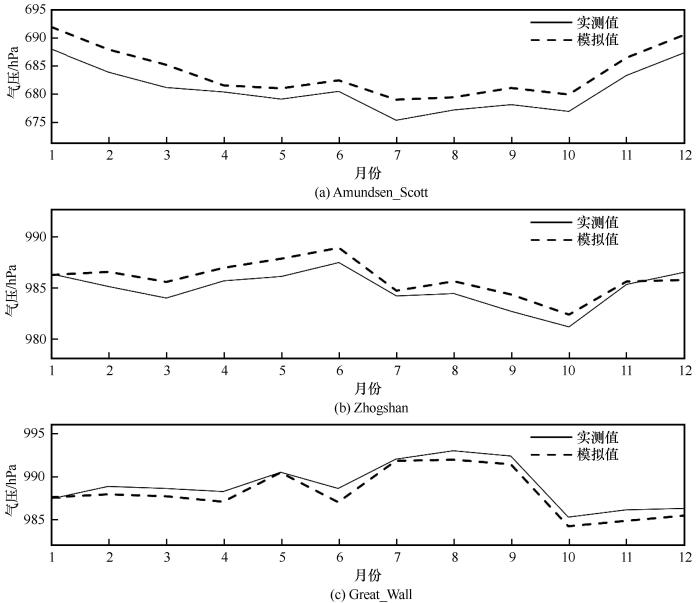
图23给出了三个代表站点近地表气压模拟值与观测值的月平均分析结果。Amundsen_Scott、Zhongshan、Great_Wall月平均近地表气压值分别在677.17~687.96 hPa、981.16~987.48 hPa、986.15~993.03 hPa,三个站点中Amundsen_Scott的变化幅度最大,Zhongshan和Great_Wall次之。与观测结果相比,Amundsen_Scott、Zhongshan的模拟气压值较实际气压偏低,而Great_Wall的模拟气压值较实际气压偏高。而从误差大小来看,各站点气压的模拟误差都较小,其中Amundsen_Scott的误差最大,其在2月误差最大,约为4.04 hPa,4—6月的误差最小,其余月份误差偏大;Zhongshan的误差次之,其在1、7、11—12月误差小于0.80 hPa,误差最小;Great_wall的误差最小,其在8月误差最大为1.04 hPa,其余月份误差都小于1.00 hPa。
图23
图23
代表站点月平均近地面气压模拟值和观测值
Fig.23
Simulated and observed monthly average near surface pressure in representative stations
3 讨论
本文统计了模式的驱动资料ERA-interim与实测值在所有月份的误差分布情况(表2)。从相关性上,部分月份的Polar WRF模拟值与观测值的相关性要略低于ERA-interim。但就从误差指标来看,模式与ERA-interim相比,其精度有了一定的提升。首先从温度上来,模式模拟结果与再分析资料相比,比较接近,模式在1月、3—7月以及9月的偏差、平均绝对误差、均方根误差要低于ERA-interim,而在8月虽然模式的偏差和平均绝对误差的误差小于ERA-interim,但是均方根误差略大,说明部分站点存在较大的误差。与温度相比,模式对再分析资料的风速和气压有明显的改进,模式在各月份的误差均小于ERA-interim。
表2 ERA-interim 2 m气温、10 m风速、地表气压月误差统计
Table 2
| 误差 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 温度 | 平均偏差 | -0.34 | -0.55 | -0.55 | -1.26 | -0.87 | -0.36 | -0.60 | -0.30 | 0.18 | 0.10 | 0.06 | -0.10 |
| 平均绝对误差 | 1.00 | 1.53 | 2.13 | 3.00 | 2.75 | 2.80 | 2.80 | 2.57 | 2.12 | 1.85 | 1.53 | 1.04 | |
| 均方根误差 | 1.36 | 2.13 | 2.95 | 3.85 | 3.62 | 3.56 | 3.82 | 3.44 | 3.18 | 2.47 | 2.10 | 1.36 | |
| 相关系数 | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 | 0.98 | 0.98 | 0.98 | 0.98 | 0.99 | 0.99 | 0.84 | |
| 风速 | 平均偏差 | 4.47 | 5.49 | 5.84 | 5.79 | 5.60 | 5.81 | 5.56 | 5.74 | 5.93 | 5.97 | 5.62 | 4.77 |
| 平均绝对误差 | 4.47 | 5.49 | 5.84 | 5.79 | 5.60 | 5.81 | 5.56 | 5.74 | 5.93 | 5.97 | 5.62 | 4.77 | |
| 均方根误差 | 5.17 | 6.41 | 6.87 | 6.89 | 6.64 | 6.83 | 6.74 | 6.81 | 6.86 | 6.85 | 6.45 | 5.43 | |
| 相关系数 | 0.84 | 0.84 | 0.85 | 0.82 | 0.86 | 0.81 | 0.84 | 0.84 | 0.79 | 0.86 | 0.85 | 0.82 | |
| 气压 | 平均偏差 | 2.72 | 2.79 | 2.91 | 2.87 | 2.98 | 2.90 | 2.91 | 2.79 | 2.76 | 2.89 | 2.74 | 2.66 |
| 平均绝对误差 | 2.63 | 2.71 | 2.90 | 2.84 | 3.00 | 2.93 | 2.97 | 2.85 | 2.82 | 2.85 | 2.71 | 2.59 | |
| 均方根误差 | 3.72 | 3.73 | 3.85 | 3.85 | 3.98 | 3.88 | 3.87 | 3.75 | 3.74 | 3.78 | 3.73 | 3.67 | |
| 相关系数 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
从模式对气温、风速、气压的模拟结果来看,模式对气压的模拟精度整体偏高。Nigro等[36]对基于Polar WRF的AMPS进行评估,认为在较长的预报时间内,模型在对气压的预测比其他气象因素更准确。Polar WRF模式对温度的模拟在沿岸以偏冷为主,而在内陆以偏暖为主,这与Tastula等[15]利用ERA-40驱动的Polar WRF3.1.1和马永锋[22]以ERA-Interim为初始场驱动的Poalr WRF3.21的模拟结果较为一致。这种冷暖偏差的区域分布与ERA-interim在南极冰盖内陆偏暖而在沿岸偏冷的现象较为一致[22],说明模式的误差一部分源自初始场资料。另一方面,Valkonen等[37]研究表明模型在云模拟方面存在一定缺陷,导致与辐射通量建模相关的问题,进而影响温度模拟。对风速的验证有必要将自动气象站的风速外推到10 m高度,在使用外推法后,所有自动气象站点的RMSE都有了明显降低。虽然误差有所降低,部分站点的风速模拟误差仍偏大,其模拟年平均值总体上低于实际风速值,且沿岸地区的误差要略大于内陆地区。Tastula等[15]的试验表明风速模拟的整体相关性偏低;Deb等[23]利用Poalr WRF3.5.1对西南极进行嵌套模拟,模拟风速与实测相比略微偏低估,且内陆地区的模拟结果更为优良,这与本文的模拟的结果较为一致。而温度的偏差一定程度上会引起风速的误差[38]。另一方面,风速在沿岸地区的误差偏大,其原因可能是由于沿岸等地区地形比较陡峭,而模拟格网无法精确地再现区域地形的复杂变化,这从一定程度上为海岸区域的风速模拟带来了误差,并且由于格网的风速值为覆盖区域风速的平均值,而风速在地理空间的变化幅度比较剧烈,因此这也会给模拟结果带来一定的误差。此外,模型的冰表面粗糙度为1 mm,高于Budd等[29]在Byrd的实测值,这也会对风速的模拟造成影响。
4 结论
本研究利用28个站点的气象观测资料验证了以ERA-interim为侧边界驱动资料的Polar WRF模式对南极冰盖2 m气温、10 m风速以及地面气压的模拟能力。具体结论如下:
(1)Polar WRF对气温、风速、气压的模拟结果在四季和各个月份误差分别小于4 ℃、2.4 hPa、4.5 m·s-1,且在2004—2013年间的模拟值与观测值的年际变化趋势大致一致,整体而言模式能够捕捉南极气温、气压和风速的年际变化特征,模拟效果较为优良。
(2)模式对年平均气温和年平均风速的模拟值和实测值在各个站点的相关性都较高,所有站点都通过了α=0.1的显著性检验,而对风速的模拟有25%的站点未通过α=0.1的显著性检验,这些站点主要分布在沿岸部分误差较大的站点。此外Polar WRF对2 m气温、近地面气压和10 m风速模拟结果的年均方根误差范围分别为1.3~5.3 ℃、1.19~5.00 hPa、1.65~8.71 m·s-1。
(3)模拟结果从空间分布来看,气温的模拟在东南极沿岸呈冷偏差,在南极内陆呈暖偏差,在南极半岛既存在冷偏差也存在暖偏差,而对气压和风速的模拟在整个南极冰盖主要呈高估。而从误差来看,模拟气温和气压在沿岸的误差低于内陆,而对风速的模拟精度在沿岸要低于内陆地区。
(4)季节上,模式对气温的模拟在夏季和秋季的模拟误差要低于春季和冬季,对风速的模拟在冬季误差最高,春秋次之,夏季最低,而对气压的模拟在冬季误差最低,秋季和夏季次之,春季误差最高。
参考文献
Automatic weather stations in the Antarctic
[J].
Changes in Antarctic Climate System: Past, present and future
[J].
南极地区气候系统变化:过去、现在和将来
[J].
Evidence of Arctic and Antarctic changes and their regulation of global climate change: further findings since the Fourth IPCC Assessment Report released
[J].
南极和北极地区变化对全球气候变化的指示和调控作用——第四次IPCC评估报告以来一些新认知
[J].
Surface contribution to planetary albedo variability in cryosphere regions
[J].
Warming of the Antarctic ice-sheet surface since the 1957 International Geophysical Year
[J].
Effects of polar ice sheets on global sea level in high-resolution greenhouse scenarios
[J].
West Antarctic ice loss influenced by internal climate variability and anthropogenic forcing
[J].
The study of ice sheet height change in Antarctic by using ICESat laser altimeter data
[D].
利用ICESAT激光测高数据监测南极冰盖高程变化的研究
[D].
Antarctic climate history over the last 100 million years
[J].
Progress in studies of cryospheric changes and their impacts on climate of China
[J].
冰冻圈变化及其对中国气候的影响
[J].
Antarctic automatic weather station program: 30 years of polar observation
[J].
Detecting trends in time series of functional data: A study of Antarctic climate change
[J].
Recent near-surface temperature trends in the Antarctic peninsula from observed, reanalysis and regional climate model data
[J].
Heat balance at the snow surface in a katabatic wind zone, east Antarctica
[J].
WRF model experiments on the Antarctic atmosphere in winter
[J].
An assessment of precipitation changes over Antarctica and the Southern Ocean since 1989 in contemporary global reanalyses
[J].
Evaluation of temperature and wind over Antarctica in a Regional Atmospheric Climate Model using 1 year of automatic weather station data and upper air observations
[J].
Development and testing of polar weather research and forecasting model: 2. Arctic Ocean
[J].
Arctic land simulations with Polar WRF
[C]//Preprints, 10th Conf.
Development and testing of polar weather research and forecasting (WRF) model. part I: Greenland ice sheet meteorology
[J].
The microphysics of clouds over the Antarctic Peninsula–Part 2: Modelling aspects within Polar WRF
[J].
Evaluation of polar WRF simulations of Antarctic atmospheric circulation
[D].
Polar WRF对南极地区天气过程的模拟试验研究
[D].
An assessment of the Polar Weather Research and Forecasting (WRF) model representation of near-surface meteorological variables over West Antarctica
[J].
A dynamical investigation of the may 2004 McMurdo Antarctica severe wind event using AMPS
[J].
Evaluation of Polar WRF forecasts on the Arctic System Reanalysis Domain: 2. Atmospheric hydrologic cycle
[J].
Dynamic Change of Totten Glacier, East Antarctica
[D].
Temperature and wind climate of the Antarctic peninsula as simulated by a high-resolution regional atmospheric climate model
[J].
A description of the advanced research WRF model version 4
[J].
Physical characteristics of the Antarctic Sea-ice zone derived from modelling and observations
[J].
Surface climate of the interior of the Lambert Glacier Basin, Antarctica, from automatic weather station data
[J].
Antarctic automatic weather station program: 30 years of polar observation
[J].
The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer
[J].
Robustness of the recent global atmospheric reanalyses for Antarctic near-surface wind speed climatology
[J].
Determining the power-law wind-profile exponent under near-neutral stability conditions at sea
[J].
A weather-pattern-based approach to evaluate the antarctic mesoscale prediction system (AMPS) forecasts: comparison to automatic weather station observations
[J].
Atmosphere-sea ice interaction in early summer in the Antarctic: Evaluation and challenges of a regional atmospheric model
[J].
Evaluation of polar MM5 simulations of Antarctic atmospheric circulation
[J].
Effects of spectral nudging in WRF on Arctic temperature and precipitation simulations
[J].


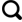



 甘公网安备 62010202000676号
甘公网安备 62010202000676号